Solved

Find the Standard Form of the Equation of the Parabola

Question 245

Multiple Choice

Find the standard form of the equation of the parabola with the given characteristic and vertex at the origin. Focus: Find the standard form of the equation of the parabola with the given characteristic and vertex at the origin. Focus: A) B) C) D) E)


A) Find the standard form of the equation of the parabola with the given characteristic and vertex at the origin. Focus: A) B) C) D) E)
B) Find the standard form of the equation of the parabola with the given characteristic and vertex at the origin. Focus: A) B) C) D) E)
C) Find the standard form of the equation of the parabola with the given characteristic and vertex at the origin. Focus: A) B) C) D) E)
D) Find the standard form of the equation of the parabola with the given characteristic and vertex at the origin. Focus: A) B) C) D) E)
E) Find the standard form of the equation of the parabola with the given characteristic and vertex at the origin. Focus: 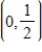A) 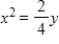B) 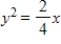C) 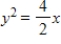D) 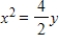E)

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q240: Convert the rectangular equation to polar form.Assume

Q241: Find the standard form of the equation

Q242: Find the angle <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB7896/.jpg" alt="Find the

Q243: Give the standard form of the equation

Q244: Consider the polar equation: ​ <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB7896/.jpg"

Q246: The equations of a parabola and a

Q247: Find a set of parametric equations for

Q248: The receiver in a parabolic satellite dish

Q249: Find the standard form of the equation

Q250: A moving conveyor is built so that