Solved

Graph the Function and Determine the Interval(s) for Which F

Question 589

Multiple Choice

Graph the function and determine the interval(s) for which f (x) ≥ 0. Graph the function and determine the interval(s) for which f (x) ≥ 0. A) B) C) D) {-2} E) Graph the function and determine the interval(s) for which f (x) ≥ 0. A) B) C) D) {-2} E)


A) Graph the function and determine the interval(s) for which f (x) ≥ 0. A) B) C) D) {-2} E)
B) Graph the function and determine the interval(s) for which f (x) ≥ 0. A) B) C) D) {-2} E)
C) Graph the function and determine the interval(s) for which f (x) ≥ 0. A) B) C) D) {-2} E)
D) {-2}
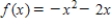
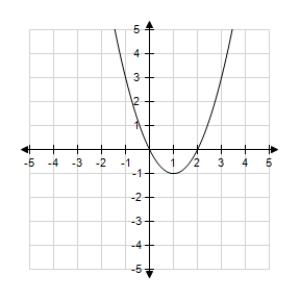
E) Graph the function and determine the interval(s) for which f (x) ≥ 0. A) 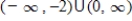B) 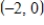C) 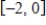D) {-2} E)

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q2: Find the x- and y-intercepts of the

Q5: Evaluate the function f(x)= 2[[x]] + 7

Q6: Find the y-intercept of the graph of

Q7: Find the coordinates of a second point

Q585: Plot the two real numbers on the

Q587: Write the standard form of the equation

Q590: Find <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB7896/.jpg" alt="Find and

Q591: Is the interval bounded or unbounded? -6

Q593: Sketch the subset on the real number

Q594: Find <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB7896/.jpg" alt="Find .