Solved

Use the Functions Given by F(x) = X + 2

Question 187

Multiple Choice

Use the functions given by f(x) = x + 2 and g(x) = 2x - 5 to find (f º g) -1. ​


A) Use the functions given by f(x) = x + 2 and g(x) = 2x - 5 to find (f <sub>º</sub> g) <sup>-1</sup>. ​ A) B) C) D) E)
B) Use the functions given by f(x) = x + 2 and g(x) = 2x - 5 to find (f <sub>º</sub> g) <sup>-1</sup>. ​ A) B) C) D) E)
C) Use the functions given by f(x) = x + 2 and g(x) = 2x - 5 to find (f <sub>º</sub> g) <sup>-1</sup>. ​ A) B) C) D) E)
D) Use the functions given by f(x) = x + 2 and g(x) = 2x - 5 to find (f <sub>º</sub> g) <sup>-1</sup>. ​ A) B) C) D) E)
E) Use the functions given by f(x) = x + 2 and g(x) = 2x - 5 to find (f <sub>º</sub> g) <sup>-1</sup>. ​ A) 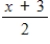B) 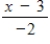C) 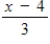D) 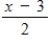E)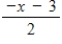

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q12: Evaluate the function f(x)= [[x]] for x

Q43: Find the slope of the line passing

Q182: Identify the rule(s) of algebra illustrated by

Q183: Evaluate the indicated function for <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB7896/.jpg"

Q184: Find the inverse of the one-to-one function.

Q185: Identify the terms.Then identify the coefficients of

Q188: Select the linear function such that it

Q189: Identify the parent function and the transformation

Q190: Find the domain of the function. ​

Q192: Change the following number from scientific notation