Solved

The Largest Open Interval Over Which F Is Concave Up

Question 46

Multiple Choice

The largest open interval over which f is concave up for f(x) = 4x3 + 8x2 - 7x + 2 is


A) The largest open interval over which f is concave up for f(x) = 4x<sup>3</sup> + 8x<sup>2</sup> - 7x + 2 is A) B) C) D) E)
B) The largest open interval over which f is concave up for f(x) = 4x<sup>3</sup> + 8x<sup>2</sup> - 7x + 2 is A) B) C) D) E)
C) The largest open interval over which f is concave up for f(x) = 4x<sup>3</sup> + 8x<sup>2</sup> - 7x + 2 is A) B) C) D) E)
D) The largest open interval over which f is concave up for f(x) = 4x<sup>3</sup> + 8x<sup>2</sup> - 7x + 2 is A) B) C) D) E)
E) The largest open interval over which f is concave up for f(x) = 4x<sup>3</sup> + 8x<sup>2</sup> - 7x + 2 is A) B) 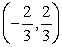C) D) E)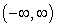

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q41: Use a graphing utility to estimate the

Q42: f(x) = cos 4x. Find the

Q43: The equation, x<sup>3</sup> - 2x - 19

Q44: Verify that f(x) = x<sup>2</sup> + 8

Q45: Use Newton's Method to find the largest

Q47: Use Newton's Method to find the largest

Q48: Find the value c that satisfies

Q49: Find the location of the absolute

Q50: Given y = x<sup>2/3</sup>(x + 4). Plot

Q51: Find all relative extrema of f(x) =