Solved

The Largest Open Interval Over Which F Is Concave Up

Question 361

Multiple Choice

The largest open interval over which f is concave up for f(x) = 6x3 + 4x2- 3x + 2 is


A) The largest open interval over which f is concave up for f(x) = 6x<sup>3</sup> + 4x<sup>2</sup>- 3x + 2 is A) B) C) D) E)
B) The largest open interval over which f is concave up for f(x) = 6x<sup>3</sup> + 4x<sup>2</sup>- 3x + 2 is A) B) C) D) E)
C) The largest open interval over which f is concave up for f(x) = 6x<sup>3</sup> + 4x<sup>2</sup>- 3x + 2 is A) B) C) D) E)
D) The largest open interval over which f is concave up for f(x) = 6x<sup>3</sup> + 4x<sup>2</sup>- 3x + 2 is A) B) C) D) E)
E) The largest open interval over which f is concave up for f(x) = 6x<sup>3</sup> + 4x<sup>2</sup>- 3x + 2 is A) 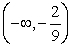B) 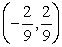C) 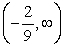D) 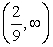E)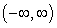

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q356: The cost of fuel used in propelling

Q357: If f(x) = x<sup>4</sup> . Use a

Q358: f(x) = 4x<sup>4</sup> - 7x<sup>5</sup> , find

Q359: If f(x) = 6x<sup>4</sup>- 4x<sup>3</sup> + 11

Q360: Let s(t) = 3t<sup>4</sup>. Find t when

Q362: A projectile is dropped, and reaches the

Q364: Given <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB6988/.jpg" alt="Given .

Q365: Let s(t) = t<sup>5</sup>- 2t + 9

Q366: Let s(t) = sin 4t be a

Q490: If f(x) = x(x - 6)<sup>2</sup> ,