Evaluate Where F(x, Y, Z) = -X I - $\sigma$

Essay

Evaluate 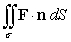where F(x, y, z) = -x i - 2x j + (z - 1)k and $\sigma$ is the surface enclosed by that portion of the paraboloid z = 4 - y² which lies in the first octant and is bounded by the coordinate planes and the plane y = x. The surface is oriented by upward unit normals.