Multiple Choice
A lamina with density (x, y) = 2x2 + y2 + 9 is bounded by x = y, x = 0, y = 0, y = 2. Find its center of mass.
A) 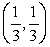
B) 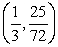
C) 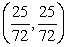
D) 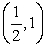
E) 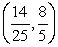
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q9: Find the Jacobian, <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB6988/.jpg" alt="Find the
Q10: Evaluate <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB6988/.jpg" alt="Evaluate by
Q11: Find <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB6988/.jpg" alt="Find where
Q12: Use a double integral in polar coordinates
Q13: Find the volume of the region bounded
Q15: Find the volume of the solid in
Q16: Find the volume of the solid enclosed
Q17: Use an appropriate transform to evaluate <img
Q18: Use a triple integral to find the
Q19: A lamina with density <span