Solved

Use Lagrange Multipliers to Find the Maximum and Minimum Values

Question 71

Multiple Choice

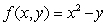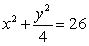Use Lagrange multipliers to find the maximum and minimum values of Use Lagrange multipliers to find the maximum and minimum values of subject to . A) The maximum value is 0, and there is no minimum value. B) The maximum value is , and the minimum value is C) The maximum value is , and the minimum value is D) The maximum value is , and the minimum value is E) There is no maximum value, and the minimum value is 0. 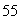subject to Use Lagrange multipliers to find the maximum and minimum values of subject to . A) The maximum value is 0, and there is no minimum value. B) The maximum value is , and the minimum value is C) The maximum value is , and the minimum value is D) The maximum value is , and the minimum value is E) There is no maximum value, and the minimum value is 0. .


A) The maximum value is 0, and there is no minimum value.
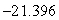
B) The maximum value is Use Lagrange multipliers to find the maximum and minimum values of subject to . A) The maximum value is 0, and there is no minimum value. B) The maximum value is , and the minimum value is C) The maximum value is , and the minimum value is D) The maximum value is , and the minimum value is E) There is no maximum value, and the minimum value is 0. , and the minimum value is
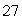Use Lagrange multipliers to find the maximum and minimum values of subject to . A) The maximum value is 0, and there is no minimum value. B) The maximum value is , and the minimum value is C) The maximum value is , and the minimum value is D) The maximum value is , and the minimum value is E) There is no maximum value, and the minimum value is 0.
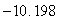
C) The maximum value is Use Lagrange multipliers to find the maximum and minimum values of subject to . A) The maximum value is 0, and there is no minimum value. B) The maximum value is , and the minimum value is C) The maximum value is , and the minimum value is D) The maximum value is , and the minimum value is E) There is no maximum value, and the minimum value is 0. , and the minimum value is
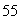Use Lagrange multipliers to find the maximum and minimum values of subject to . A) The maximum value is 0, and there is no minimum value. B) The maximum value is , and the minimum value is C) The maximum value is , and the minimum value is D) The maximum value is , and the minimum value is E) There is no maximum value, and the minimum value is 0.
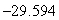
D) The maximum value is Use Lagrange multipliers to find the maximum and minimum values of subject to . A) The maximum value is 0, and there is no minimum value. B) The maximum value is , and the minimum value is C) The maximum value is , and the minimum value is D) The maximum value is , and the minimum value is E) There is no maximum value, and the minimum value is 0. , and the minimum value is
Use Lagrange multipliers to find the maximum and minimum values of subject to . A) The maximum value is 0, and there is no minimum value. B) The maximum value is , and the minimum value is C) The maximum value is , and the minimum value is D) The maximum value is , and the minimum value is E) There is no maximum value, and the minimum value is 0.
E) There is no maximum value, and the minimum value is 0.

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q66: Let <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB6988/.jpg" alt="Let .

Q67: Evaluate <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB6988/.jpg" alt="Evaluate .

Q68: Find the local linear approximation to <img

Q69: Use Lagrange multipliers to find all the

Q70: Let <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB6988/.jpg" alt="Let Find

Q72: (x<sup>2</sup> + y<sup>2</sup> + z<sup>2</sup>)<sup>5</sup> = -23.

Q73: Let <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB6988/.jpg" alt="Let ;

Q74: Determine whether the function <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB6988/.jpg" alt="Determine

Q75: Let <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB6988/.jpg" alt="Let ;

Q76: Let <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB6988/.jpg" alt="Let .