Solved

A Rectangular Box, Open at the Top, Is to Contain

Question 106

Multiple Choice

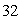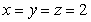A rectangular box, open at the top, is to contain A rectangular box, open at the top, is to contain cubic inches. Find the dimensions of the box for which the surface area is a minimum. A) in B) C) D) E) cubic inches. Find the dimensions of the box for which the surface area is a minimum.


A) A rectangular box, open at the top, is to contain cubic inches. Find the dimensions of the box for which the surface area is a minimum. A) in B) C) D) E) in
B) A rectangular box, open at the top, is to contain cubic inches. Find the dimensions of the box for which the surface area is a minimum. A) in B) C) D) E)
C) A rectangular box, open at the top, is to contain cubic inches. Find the dimensions of the box for which the surface area is a minimum. A) in B) C) D) E)
A rectangular box, open at the top, is to contain cubic inches. Find the dimensions of the box for which the surface area is a minimum. A) in B) C) D) E)
D) A rectangular box, open at the top, is to contain cubic inches. Find the dimensions of the box for which the surface area is a minimum. A) in B) C) D) E)
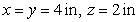
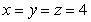
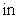
E) A rectangular box, open at the top, is to contain cubic inches. Find the dimensions of the box for which the surface area is a minimum. A) in B) C) D) 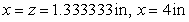E)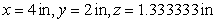

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q101: Evaluate <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB6988/.jpg" alt="Evaluate .

Q102: Evaluate <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB6988/.jpg" alt="Evaluate ."

Q103: Let f(x, y) = x<sup>2</sup> + xy

Q104: The legs of a right triangle are

Q105: Let <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB6988/.jpg" alt="Let ;

Q107: Evaluate <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB6988/.jpg" alt="Evaluate ."

Q108: Use the chain rule to find <img

Q109: The lengths and widths of a rectangle

Q110: Let <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB6988/.jpg" alt="Let .

Q111: Let <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB6988/.jpg" alt="Let .