Solved

Use the Total Differential to Approximate the Change in

Question 43

Multiple Choice

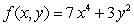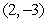Use the total differential to approximate the change in Use the total differential to approximate the change in as (x, y) varies from to . A) B) C) D) E) as (x, y) varies from Use the total differential to approximate the change in as (x, y) varies from to . A) B) C) D) E) to Use the total differential to approximate the change in as (x, y) varies from to . A) B) C) D) E) .


A) Use the total differential to approximate the change in as (x, y) varies from to . A) B) C) D) E)
B) Use the total differential to approximate the change in as (x, y) varies from to . A) B) C) D) E)
C) Use the total differential to approximate the change in as (x, y) varies from to . A) B) C) D) E)
D) Use the total differential to approximate the change in as (x, y) varies from to . A) B) C) D) E)
E) Use the total differential to approximate the change in as (x, y) varies from to 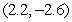. A) 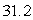B) 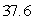C) 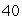D) 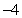E)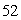

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q38: Use Lagrange multipliers to find the maximum

Q39: Find parametric equations for the normal line

Q40: Find d <span class="ql-formula" data-value="

Q41: Let <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB6988/.jpg" alt="Let .

Q42: At t = 0, the position of

Q44: Find the slope of the surface <img

Q45: Determine whether the limit exists. If so,

Q46: The sides of a rectangle are measured

Q47: Use the chain rule to find <img

Q48: Let <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB6988/.jpg" alt="Let .