Multiple Choice
Let z = 5 + 4 sin(x2y4) . Find 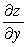 .
.
A) 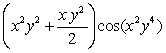
B) 2xy3 cos(x2y4)
C) y3 cos(x2y4)
D) 16x2y3 cos(x2y4)
E) x2 cos(x2y4)
Correct Answer:

Verified
Correct Answer:
Verified
Q30: Let <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB6988/.jpg" alt="Let ;
Q31: Use the chain rule to find <img
Q32: Let <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB6988/.jpg" alt="Let .
Q33: A rectangular box is to contain <img
Q34: Evaluate <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB6988/.jpg" alt="Evaluate ."
Q36: Sketch the graph of <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB6988/.jpg" alt="Sketch
Q37: Find the equations of the tangent plane
Q38: Use Lagrange multipliers to find the maximum
Q39: Find parametric equations for the normal line
Q40: Find d <span class="ql-formula" data-value="