Essay
Evaluate 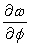 at the point whose spherical coordinates are
at the point whose spherical coordinates are 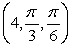 if = (x2 - 2y + z)2 and x = sin cos , y = sin sin , z = cos .
if = (x2 - 2y + z)2 and x = sin cos , y = sin sin , z = cos .
Correct Answer:

Verified
Correct Answer:
Verified
Q169: Evaluate <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB6988/.jpg" alt="Evaluate .
Q170: Let <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB6988/.jpg" alt="Let .
Q171: Find an equation for the tangent plane
Q172: Let <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB6988/.jpg" alt="Let .
Q173: Let <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB6988/.jpg" alt="Let .
Q175: Find the rate of change of <img
Q176: Let <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB6988/.jpg" alt="Let .
Q177: An open rectangular box is to contain
Q178: Let <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB6988/.jpg" alt="Let .
Q179: Let <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB6988/.jpg" alt="Let .