Multiple Choice
To prove that 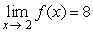 , where
, where 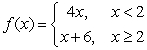 , a reasonable relationship between and would be
, a reasonable relationship between and would be
A) = 4
B) = 
C) = 4 + 6
D) = 2
E) 
Correct Answer:

Verified
Correct Answer:
Verified
Q103: Find the limit. <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB6988/.jpg" alt="
Q104: Find <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB6988/.jpg" alt="Find ."
Q105: Find a least number
Q106: Let <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB6988/.jpg" alt="Let .
Q107: Find <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB6988/.jpg" alt="Find ."
Q109: Find a least number <span
Q110: Determine if the discontinuity at x =
Q111: Approximate the horizontal asymptote of <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB6988/.jpg"
Q112: Define <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB6988/.jpg" alt="Define so
Q113: Assign a value to the constant k