Consider the Following Set of Quarterly Sales Data, Given in Thousands

Short Answer

Consider the following set of quarterly sales data, given in thousands of dollars.
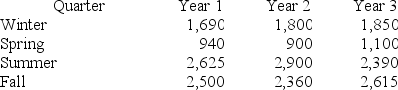The following dummy variable model that incorporates a linear trend and constant seasonal variation was used: y(t) = β₀ + β_1t + β_Q1(Q1) + β_Q2(Q2) + β_Q3(Q3) + E_t. In this model, there are three binary seasonal variables (Q1, Q2, and Q3), where Qi is a binary (0,1) variable defined as:
Qi = 1, if the time series data is associated with quarter i;
Qi = 0, if the time series data is not associated with quarter i.
The results associated with this data and model are given in the following Minitab computer output.
The regression equation is
Sales = 2442 + 6.2 Time − 693 Q1 − 1499 Q2 + 153 Q3
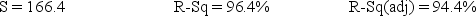Analysis of Variance
At α = .05, test the significance of the model.