Solved

Consider the Quarterly Production Data (In Thousands of Units) for the XYZ

Question 40

Short Answer

Consider the quarterly production data (in thousands of units) for the XYZ manufacturing company below. The normalized (adjusted) seasonal factors are winter = .9982, spring = .9263, summer = 1.139, and fall = .9365.
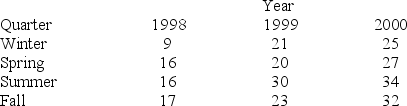Consider the quarterly production data (in thousands of units) for the XYZ manufacturing company below. The normalized (adjusted) seasonal factors are winter = .9982, spring = .9263, summer = 1.139, and fall = .9365. Based on the following deseasonalized observations (d<sub>t</sub>), a trend line was estimated. The linear regression trend equation is tr<sub>t</sub> = 10.1 + 1.91(t). Based on this trend equation, the following trend values are calculated for each period in the time series. Year 1998 Year 1999 Year 2000 Isolate the cyclical and irregular components by calculating the estimate of CL<sub>t</sub> × IR<sub>t</sub> for the first four quarters in the time series. Based on the following deseasonalized observations (dt), a trend line was estimated. The linear regression trend equation is trt = 10.1 + 1.91(t). Based on this trend equation, the following trend values are calculated for each period in the time series.
Year
1998
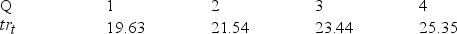Consider the quarterly production data (in thousands of units) for the XYZ manufacturing company below. The normalized (adjusted) seasonal factors are winter = .9982, spring = .9263, summer = 1.139, and fall = .9365. Based on the following deseasonalized observations (d<sub>t</sub>), a trend line was estimated. The linear regression trend equation is tr<sub>t</sub> = 10.1 + 1.91(t). Based on this trend equation, the following trend values are calculated for each period in the time series. Year 1998 Year 1999 Year 2000 Isolate the cyclical and irregular components by calculating the estimate of CL<sub>t</sub> × IR<sub>t</sub> for the first four quarters in the time series. Year
1999
Consider the quarterly production data (in thousands of units) for the XYZ manufacturing company below. The normalized (adjusted) seasonal factors are winter = .9982, spring = .9263, summer = 1.139, and fall = .9365. Based on the following deseasonalized observations (d<sub>t</sub>), a trend line was estimated. The linear regression trend equation is tr<sub>t</sub> = 10.1 + 1.91(t). Based on this trend equation, the following trend values are calculated for each period in the time series. Year 1998 Year 1999 Year 2000 Isolate the cyclical and irregular components by calculating the estimate of CL<sub>t</sub> × IR<sub>t</sub> for the first four quarters in the time series. Year
2000
Consider the quarterly production data (in thousands of units) for the XYZ manufacturing company below. The normalized (adjusted) seasonal factors are winter = .9982, spring = .9263, summer = 1.139, and fall = .9365. Based on the following deseasonalized observations (d<sub>t</sub>), a trend line was estimated. The linear regression trend equation is tr<sub>t</sub> = 10.1 + 1.91(t). Based on this trend equation, the following trend values are calculated for each period in the time series. Year 1998 Year 1999 Year 2000 Isolate the cyclical and irregular components by calculating the estimate of CL<sub>t</sub> × IR<sub>t</sub> for the first four quarters in the time series. Isolate the cyclical and irregular components by calculating the estimate of CLt × IRt for the first four quarters in the time series.

Correct Answer:

verifed

Verified

.75, 1.242, .888, 1....

View Answer

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q35: Consider the quarterly production data (in thousands

Q36: Two forecasting models were used to predict

Q37: Based on the following data, a forecaster

Q38: When using simple exponential smoothing, the more

Q39: A simple index is computed by using

Q41: In general, the number of dummy variables

Q42: Random shock is a value that is

Q43: Since a(n) _ index employs the base-period

Q44: Two forecasting models were used to predict

Q45: Weighting in exponential smoothing is accomplished by