Solved

Given Two Independent Normal Distributions with S12 − S22= 100

Question 57

Multiple Choice

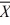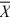Given two independent normal distributions with s12 − s22= 100, μ1 = μ2 = 50, and n1 = n2 = 50, the sampling distribution of the mean difference Given two independent normal distributions with s<sub>1</sub><sup>2</sup> − s<sub>2</sub><sup>2</sup>= 100, μ<sub>1</sub> = μ<sub>2</sub> = 50, and n<sub>1</sub> = n<sub>2</sub> = 50, the sampling distribution of the mean difference <sub>1</sub> − <sub>2</sub> will have a mean of ________. A) 100 B) 1 C) 0 D) 50 E) 10 1 − Given two independent normal distributions with s<sub>1</sub><sup>2</sup> − s<sub>2</sub><sup>2</sup>= 100, μ<sub>1</sub> = μ<sub>2</sub> = 50, and n<sub>1</sub> = n<sub>2</sub> = 50, the sampling distribution of the mean difference <sub>1</sub> − <sub>2</sub> will have a mean of ________. A) 100 B) 1 C) 0 D) 50 E) 10 2 will have a mean of ________.


A) 100
B) 1
C) 0
D) 50
E) 10

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q52: Find a 95 percent confidence interval for

Q53: In an opinion survey, a random sample

Q54: We use the following data for a

Q55: Find a 98 percent confidence interval for

Q56: When testing H<sub>0</sub>: σ<sub>1</sub><sup>2</sup> ≤ σ<sub>2</sub><sup>2</sup> and

Q58: In testing the difference between two population

Q59: In general, the shape of the F

Q60: An independent samples experiment is an experiment

Q61: Two hospital emergency rooms use different procedures

Q62: The controller of a chain of toy