Solved

When We Test H0: μ1 ≤ μ2, HA: μ1 >

Question 34

Short Answer

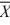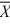When we test H0: μ1 ≤ μ2, HA: μ1 > μ2 at α = .10, where When we test H<sub>0</sub>: μ<sub>1</sub> ≤ μ<sub>2</sub>, H<sub>A</sub>: μ<sub>1</sub> > μ<sub>2</sub> at α = .10, where <sub>1</sub> = 77.4, <sub>2</sub> = 72.2, s<sub>1</sub> = 3.3, s<sub>2</sub> = 2.1, n<sub>1</sub> = 6, and n<sub>2</sub> = 6, can we reject the null hypothesis (using critical value rules)? (Assume equal variances.) 1 = 77.4, When we test H<sub>0</sub>: μ<sub>1</sub> ≤ μ<sub>2</sub>, H<sub>A</sub>: μ<sub>1</sub> > μ<sub>2</sub> at α = .10, where <sub>1</sub> = 77.4, <sub>2</sub> = 72.2, s<sub>1</sub> = 3.3, s<sub>2</sub> = 2.1, n<sub>1</sub> = 6, and n<sub>2</sub> = 6, can we reject the null hypothesis (using critical value rules)? (Assume equal variances.) 2 = 72.2, s1 = 3.3,
s2 = 2.1, n1 = 6, and n2 = 6, can we reject the null hypothesis (using critical value rules)? (Assume equal variances.)

Correct Answer:

verifed

Verified

Reject the null hypothesis since our cal...

View Answer

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q29: An experiment in which there is no

Q30: In testing the difference between the means

Q31: Testing H<sub>0</sub>: σ<sub>1</sub><sup>2</sup> ≤ σ<sub>2</sub><sup>2</sup>, H<sub>A</sub>: σ<sub>1</sub><sup>2</sup>

Q32: When we test H<sub>0</sub>: μ<sub>1</sub> − μ<sub>2</sub>

Q33: A test of driving ability is given

Q35: In an opinion survey, a random sample

Q36: Given the following information about a hypothesis

Q37: In order to test the effectiveness of

Q38: When comparing two independent population variances, the

Q39: In testing the difference between the means