Solved

When We Test H0: μ1 ≤ μ2, HA: μ1 >

Question 71

Short Answer

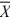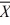When we test H0: μ1 ≤ μ2, HA: μ1 > μ2 at α = .10, where When we test H<sub>0</sub>: μ<sub>1</sub> ≤ μ<sub>2</sub>, H<sub>A</sub>: μ<sub>1</sub> > μ<sub>2</sub> at α = .10, where <sub>1</sub> = 77.4, <sub>2</sub> = 72.2, s<sub>1</sub> = 3.3, s<sub>2</sub> = 2.1, n<sub>1</sub> = 6, and n<sub>2</sub> = 6, what is the estimated pooled variance? 1 = 77.4, When we test H<sub>0</sub>: μ<sub>1</sub> ≤ μ<sub>2</sub>, H<sub>A</sub>: μ<sub>1</sub> > μ<sub>2</sub> at α = .10, where <sub>1</sub> = 77.4, <sub>2</sub> = 72.2, s<sub>1</sub> = 3.3, s<sub>2</sub> = 2.1, n<sub>1</sub> = 6, and n<sub>2</sub> = 6, what is the estimated pooled variance? 2 = 72.2, s1 = 3.3,
s2 = 2.1, n1 = 6, and n2 = 6, what is the estimated pooled variance?

Correct Answer:

verifed

Verified

The pooled variance is = 7.65....

View Answer

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q66: A coffee shop franchise owner is looking

Q67: When we test H<sub>0</sub>: p<sub>1</sub> − p<sub>2</sub>

Q68: When testing H<sub>0</sub>: μ<sub>1</sub> − μ<sub>2</sub> =

Q69: Let p<sub>1</sub> represent the population proportion of

Q70: Find a 95 percent confidence interval for

Q72: When testing the difference between two population

Q73: Suppose that a realtor is interested in

Q74: In an opinion survey, a random sample

Q75: If the limits of the confidence interval

Q76: A test of driving ability is given