Solved

Find a 95 Percent Confidence Interval for the Difference Between

Question 95

Short Answer

Find a 95 percent confidence interval for the difference between means, where n1 = 50,
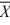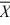n2 = 36, Find a 95 percent confidence interval for the difference between means, where n<sub>1</sub> = 50, n<sub>2</sub> = 36, <sub>1</sub> = 80, <sub>2</sub> = 75, s<sub>1</sub><sup>2</sup> = 5, and s<sub>2</sub><sup>2</sup> = 3. Assume unequal variances. 1 = 80, Find a 95 percent confidence interval for the difference between means, where n<sub>1</sub> = 50, n<sub>2</sub> = 36, <sub>1</sub> = 80, <sub>2</sub> = 75, s<sub>1</sub><sup>2</sup> = 5, and s<sub>2</sub><sup>2</sup> = 3. Assume unequal variances. 2 = 75, s12 = 5, and s22 = 3. Assume unequal variances.

Correct Answer:

verifed

Verified

[4.15, 5.85]
df = (5/50 + 3/36...

View Answer

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q90: Let p<sub>1</sub> represent the population proportion of

Q91: A fast-food company uses two management-training methods.

Q92: Find a 95 percent confidence interval for

Q93: In forming a confidence interval for μ<sub>1</sub>

Q94: A market research study conducted by a

Q96: A fast-food company uses two management-training methods.

Q97: When testing H<sub>0</sub>: σ<sub>1</sub><sup>2</sup> ≤ σ<sub>2</sub><sup>2</sup> and

Q98: A coffee shop franchise owner is looking

Q99: In testing the difference between two independent

Q100: We are testing the hypothesis that the