A Local Parent Group Was Concerned with the Increasing Cost

Multiple Choice

A local parent group was concerned with the increasing cost of school for families with school aged children.The parent group was interested in understanding the relationship between the academic grade level for the child and the total costs spent per child per academic year.They performed a multiple regression analysis using total cost as the dependent variable and academic year (x₁) as the independent variables.The multiple regression analysis produced the following tables. $$\begin{array} { | c | c | c | c | c | } \hline & \text { Coefficients } & \text { Stardard Error } & t \text { Statistic } & p \text {-value } \\\hline \text { Intercept } & 707.9144 & 435.1183 & 1.626947 & 0.114567 \\\hline \boldsymbol { x } _ { 1 } & 2.903307 & 81.62802 & 0.035568 & 0.971871 \\\hline \mathbf { x } _ { 1 } { } ^ { 2 } & 11.91297 & 3.806211 & 3.129878 & 0.003967 \\\hline\end{array}$$ $$\begin{array} { | c | c | c | c | c | c | } \hline & \text { Df } & \text { SS } & \text { MS } & F & p \text {-value } \\\hline \text { Regression } & 2 & 32055153 & 16027577 & 47.34557 & 1.49 \mathrm { E } - 09 \\\hline \text { Residual } & 27 & 9140128 & 338523.3 & & \\\hline \text { Total } & 29 & 41195281 & & & \\\hline\end{array}$$ The regression equation for this analysis is ____________.

A) 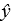= 707.9144 + 2.903307 x₁ + 11.91297 x₁²
B) 11efcd21_6411_aee5_b057_4518c9fddc20_TB7041_00= 707.9144 + 435.1183 x₁ + 1.626947 x₁²
C) 11efcd21_6411_aee5_b057_4518c9fddc20_TB7041_00 = 435.1183 + 81.62802 x₁ + 3.806211 x₁²
D) 11efcd21_6411_aee5_b057_4518c9fddc20_TB7041_00 = 1.626947 + 0.035568 x₁ + 3.129878 x₁²
E) 11efcd21_6411_aee5_b057_4518c9fddc20_TB7041_00 = 1.626947 + 0.035568 x₁ - 3.129878 x₁²