Alan Bissell, a Market Analyst for City Sound Online Mart

Multiple Choice

Alan Bissell, a market analyst for City Sound Online Mart, is analyzing sales from heavy metal song downloads.Alan's dependent variable is annual heavy metal song download sales (in $1,000,000's) , and his independent variables are website visitors (in 1,000's) and type of download format requested (0 = MP3, 1 = other) .Regression analysis of the data yielded the following tables. $$\begin{array} { | c | c | c | c | c | } \hline & \text { Coefficients } & \begin{array} { c } \text { Stardard } \\\text { Error }\end{array} & \boldsymbol { t } \text { Statistic } & p \text {-value } \\\hline \text { Intercept } & 1.7 & 0.384212 & 4.424638 & 0.00166 \\\hline \boldsymbol { x } _ { 1 } \text { (website visitors) } & 0.04 & 0.014029 & \mathbf { 2 . 8 5 1 1 4 6 } & 0.019054 \\\hline \mathbf { x } _ { 2 } \text { (download fommat) } & - 1.5666667 & 0.20518 & - 7.63558 & \mathbf { 3 . 2 1 E - 0 5 } \\\hline\end{array}$$ Alan's model is ________________.

A) 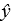= 1.7 + 0.384212 x₁ + 4.424638 x₂ + 0.00166 x₃
B) 11efcd21_6411_aee5_b057_4518c9fddc20_TB7041_00 = 1.7 + 0.04 x₁ + 1.5666667 x₂
C) 11efcd21_6411_aee5_b057_4518c9fddc20_TB7041_00 = 0.384212 + 0.014029 x₁ + 0.20518 x₂
D) 11efcd21_6411_aee5_b057_4518c9fddc20_TB7041_00 = 4.424638 + 2.851146 x₁ - 7.63558 x₂
E) 11efcd21_6411_aee5_b057_4518c9fddc20_TB7041_00 = 1.7 + 0.04 x₁ - 1.5666667 x₂