Abby Kratz, a Market Specialist at the Market Research Firm

Multiple Choice

Abby Kratz, a market specialist at the market research firm of Saez, Sikes, and Spitz, is analyzing household budget data collected by her firm.Abby's dependent variable is monthly household expenditures on groceries (in $'s) , and her independent variable is annual household income (in $1,000's) .Regression analysis of the data yielded the following tables. $\begin{array}{|c|c|c|c|c|}\hline \text { Source } & \text { df } & \text { SS } & \text { MS } & F \\\hline \text { Regresssumm } & 1 & 7685099 & 1685099 & 19.3444 \\\hline \text { Residual } & 9 & 7839.915 & 871.1017 & \\\hline \text { Total } & 10 & 24690.91 & & \\\hline\end{array}$
$$\begin{array} { | l | } \hline S _ { \mathrm { d } } = 29.51448 \\\hline r ^ { 2 } = 0.682478 \\\hline\end{array}$$ Abby's regression model is __________.
A) 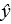$\begin{array}{|c|c|c|c|c|}\hline \text { Source } & \text { df } & \text { SS } & \text { MS } & F \\\hline \text { Regresssumm } & 1 & 7685099 & 1685099 & 19.3444 \\\hline \text { Residual } & 9 & 7839.915 & 871.1017 & \\\hline \text { Total } & 10 & 24690.91 & & \\\hline\end{array}$
$$\begin{array} { | l | } \hline S _ { \mathrm { d } } = 29.51448 \\\hline r ^ { 2 } = 0.682478 \\\hline\end{array}$$ Abby's regression model is __________.
A) 11efcd22_8a09_b9c8_b057_7d6699c46fc2_TB7041_00 = 39.15 + 2.79x
B) 11efcd22_8a09_b9c8_b057_7d6699c46fc2_TB7041_00= 39.15 - 1.79x
C) 11efcd22_8a09_b9c8_b057_7d6699c46fc2_TB7041_00 = 1.79 + 39.15x
D) 11efcd22_8a09_b9c8_b057_7d6699c46fc2_TB7041_00 = -1.79 + 39.15x
E) 11efcd22_8a09_b9c8_b057_7d6699c46fc2_TB7041_00 = 39.15 + 1.79xs) , and her independent variable is annual household income (in $1,000's) .Regression analysis of the data yielded the following tables. \begin{array}{|c|c|c|c|c|} \hline \text { Source } & \text { df } & \text { SS } & \text { MS } & F \\ \hline \text { Regresssumm } & 1 & 7685099 & 1685099 & 19.3444 \\ \hline \text { Residual } & 9 & 7839.915 & 871.1017 & \\ \hline \text { Total } & 10 & 24690.91 & & \\ \hline \end{array} \begin{array} { | l | } \hline S _ { \mathrm { d } } = 29.51448 \\ \hline r ^ { 2 } = 0.682478 \\ \hline \end{array} Abby's regression model is __________. A) = 39.15 + 2.79x B) = 39.15 - 1.79x C) = 1.79 + 39.15x D) = -1.79 + 39.15x E) = 39.15 + 1.79x " class="answers-bank-image d-block" rel="preload" > = 39.15 + 2.79x
B) 11efcd22_8a09_b9c8_b057_7d6699c46fc2_TB7041_00= 39.15 - 1.79x
C) 11efcd22_8a09_b9c8_b057_7d6699c46fc2_TB7041_00 = 1.79 + 39.15x
D) 11efcd22_8a09_b9c8_b057_7d6699c46fc2_TB7041_00 = -1.79 + 39.15x
E) 11efcd22_8a09_b9c8_b057_7d6699c46fc2_TB7041_00 = 39.15 + 1.79xs) , and her independent variable is annual household income (in $1,000's) .Regression analysis of the data yielded the following tables. \begin{array}{|c|c|c|c|c|} \hline \text { Source } & \text { df } & \text { SS } & \text { MS } & F \\ \hline \text { Regresssumm } & 1 & 7685099 & 1685099 & 19.3444 \\ \hline \text { Residual } & 9 & 7839.915 & 871.1017 & \\ \hline \text { Total } & 10 & 24690.91 & & \\ \hline \end{array} \begin{array} { | l | } \hline S _ { \mathrm { d } } = 29.51448 \\ \hline r ^ { 2 } = 0.682478 \\ \hline \end{array} Abby's regression model is __________. A) = 39.15 + 2.79x B) = 39.15 - 1.79x C) = 1.79 + 39.15x D) = -1.79 + 39.15x E) = 39.15 + 1.79x " class="answers-bank-image d-block" rel="preload" > $\begin{array}{|c|c|c|c|c|}\hline \text { Source } & \text { df } & \text { SS } & \text { MS } & F \\\hline \text { Regresssumm } & 1 & 7685099 & 1685099 & 19.3444 \\\hline \text { Residual } & 9 & 7839.915 & 871.1017 & \\\hline \text { Total } & 10 & 24690.91 & & \\\hline\end{array}$
$$\begin{array} { | l | } \hline S _ { \mathrm { d } } = 29.51448 \\\hline r ^ { 2 } = 0.682478 \\\hline\end{array}$$ Abby's regression model is __________.

A) 11efcd22_8a09_b9c8_b057_7d6699c46fc2_TB7041_00 = 39.15 + 2.79x
B) 11efcd22_8a09_b9c8_b057_7d6699c46fc2_TB7041_00= 39.15 - 1.79x
C) 11efcd22_8a09_b9c8_b057_7d6699c46fc2_TB7041_00 = 1.79 + 39.15x
D) 11efcd22_8a09_b9c8_b057_7d6699c46fc2_TB7041_00 = -1.79 + 39.15x
E) 11efcd22_8a09_b9c8_b057_7d6699c46fc2_TB7041_00 = 39.15 + 1.79x