Solved

Consider the Following Conditional Variance Equation for a GJR Model α\alpha

Question 2

Multiple Choice

Consider the following conditional variance equation for a GJR model. ht 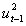= α\alpha 0 + α\alpha 1+ β\beta ht-1+ γ\gamma ut-12It-1 Consider the following conditional variance equation for a GJR model. h<sub>t</sub> = \alpha <sub>0</sub> + \alpha <sub>1</sub>+ \beta h<sub>t</sub><sub>-1</sub>+ \gamma u<sub>t</sub><sub>-1</sub><sup>2</sup>I<sub>t</sub><sub>-1</sub> where I<sub>t</sub><sub>-1</sub> = 1 if u<sub>t</sub><sub>-1</sub> < 0 = 0 otherwise For there to be evidence of a leverage effect, which one of the following conditions must hold? A) \alpha <sub>0</sub> positive and statistically significant B) \gamma positive and statistically significant C) \gamma statistically significantly greater than \alpha <sub>0</sub> D) \alpha <sub>1</sub>+ \beta statistically significantly less than \gamma where It-1 = 1 if ut-1 < 0 = 0 otherwise
For there to be evidence of a leverage effect, which one of the following conditions must hold?


A) α\alpha 0 positive and statistically significant
B) γ\gamma positive and statistically significant
C) γ\gamma statistically significantly greater than α\alpha 0
D) α\alpha 1+ β\beta statistically significantly less than γ\gamma

Correct Answer:

verifed

Verified

Related Questions

Q1: Which one of the following problems in

Q3: Assume that you have estimated a GJR

Q4: Which of the following is the most

Q5: What is an appropriate approach to testing

Q6: Which of these cannot be used to

Q7: Which of the following is true about

Q8: What would typically be the shape of

Q9: Which of these is an appropriate technique

Q10: Volatility clustering is<br>A) The tendency for financial

Q11: Suppose that a researcher wanted to obtain