Solved

A Population P Grows So That We Can Always Get

Question 3

Multiple Choice

A population P grows so that we can always get next year's population from this year's population by multiplying by 1.52.The initial population is 569.The population after t years is given by ​


A) A population P grows so that we can always get next year's population from this year's population by multiplying by 1.52.The initial population is 569.The population after t years is given by ​ A) B) C) D)
B) A population P grows so that we can always get next year's population from this year's population by multiplying by 1.52.The initial population is 569.The population after t years is given by ​ A) B) C) D)
C) A population P grows so that we can always get next year's population from this year's population by multiplying by 1.52.The initial population is 569.The population after t years is given by ​ A) B) C) D)
D) A population P grows so that we can always get next year's population from this year's population by multiplying by 1.52.The initial population is 569.The population after t years is given by ​ A) 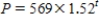B) 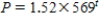C) 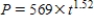D)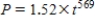

Correct Answer:

verifed

Verified

Related Questions

Q1: Solve the equation <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB7296/.jpg" alt="Solve the

Q2: Solve the exponential equation <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB7296/.jpg" alt="Solve

Q4: Next year's value of quantity 1 is

Q5: Solve the equation <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB7296/.jpg" alt="Solve the

Q6: A graph showing exponential decay is concave

Q7: A radioactive substance is decaying exponentially with

Q8: Solve the inequality <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB7296/.jpg" alt="Solve the

Q9: Over a certain time period the price

Q10: A radioactive substance is decaying exponentially with

Q11: Select the graph of <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB7296/.jpg" alt="Select