A Company Is Planning Production for the Next 4 Quarters

Essay

A company is planning production for the next 4 quarters. They want to minimize the cost of production. The production cost, demand and production capacity vary from quarter to quarter. The maximum amount of inventory which can be held is 100 units and management wants to keep at least 50 units on hand. Quarterly inventory holding cost is 4% of the cost of production. There are currently 50 units in inventory. The company wants to produce at no less than one half of its maximum capacity in any quarter.
$$\begin{array}{l}\text {\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad Quarter }\\\begin{array} { l c c c c } & 1 & 2 & 3 & 4 \\\hline \text { Unit Production Cost } & \$ 55 & \$ 50 & \$ 50 & \$ 45 \\\text { Units Demanded } & 100 & 150 & 180 & 120 \\\text { Maramum Praduction } & 150 & 150 & 160 & 130 \\\text { Holding cost } & \$ 2.2 & \$ 2 & \$ 2 & \$ 1.8\end{array}\end{array}$$ $\begin{array} { l } \text { Let } \quad P _ { i } = \text { number of units produced in quarter } i , i = 1 , \ldots , 4 \\\mathbf { B } _ { i } = \text { beginning inventory far quarter } i \\\end{array}$

$\begin{array}{ll}\text { MIN: } & 55 \mathrm{P}_{1}+50 \mathrm{P}_{2}+50 \mathrm{P}_{3}+45 \mathrm{P}_{4}+ \\& 2.2\left(\mathrm{~B}_{1}+\mathrm{B}_{2}\right) / 2+2\left(\mathrm{~B}_{2}+\mathrm{B}_{3}\right) / 2+2\left(\mathrm{~B}_{3}+\mathrm{B}_{4}\right) / 2+1.8\left(\mathrm{~B}_{4}+\mathrm{B}_{5}\right) / 2 \\\text { Subject to: } & 75 \leq \mathrm{P}_{1} \leq 150 \\&75 \leq \mathrm{P}_{2} \leq 150 \\& 80 \leq \mathrm{P}_{3} \leq 160 \\& 65 \leq \mathrm{P}_{4} \leq 130 \\& 50 \leq \mathrm{B}_{1}+\mathrm{P}_{1}-100 \leq 100 \\& 50 \leq \mathrm{B}_{2}+\mathrm{P}_{2}-150 \leq 100 \\& 50 \leq \mathrm{B}_{3}+\mathrm{P}_{3}-180 \leq 100 \\& 50 \leq \mathrm{B}_{4}+\mathrm{P}_{4}-120 \leq 100 \\&\mathrm{~B}_{2}=\mathrm{B}_{1}+\mathrm{P}_{1}-100 \\& \mathrm{~B}_{3}=\mathrm{B}_{2}+\mathrm{P}_{2}-150 \\&\mathrm{~B}_{4}=\mathrm{B}_{3}+\mathrm{P}_{3}-180 \\& \mathrm{~B}_{5}=\mathrm{B}_{4}+\mathrm{P}_{4}-120 \\& \mathrm{P}_{\mathrm{i}} \mathrm{B}_{\mathrm{i}} \geq 0\end{array}$ 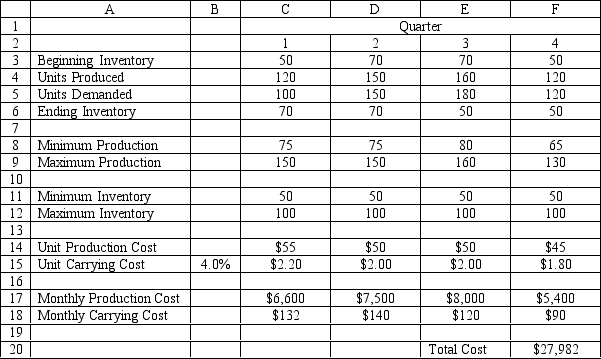What formulas are required for cells D3, D6, D8, D15, D17 and D18 in the Excel spreadsheet implementation of the formulation?