A Cellular Phone Company Wants to Locate Two New Communications $\quad$

Essay

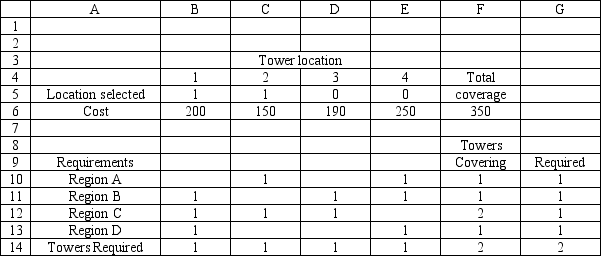
A cellular phone company wants to locate two new communications towers to cover 4 regions. The company wants to minimize the cost of installing the two towers. The regions that can be covered by each tower site are indicated by a 1 in the following table:
$\quad$$\quad$$\quad$$\quad$$\quad$$\quad$$\quad$$\quad$$\quad$$\quad$$\underline{\text { Tower Sites }}$
$\begin{array}{ccccc}\text { Region } & 1 & 2 & 3 & 4 \\\hline \text { A } & & 1 & & 1 \\\text { B } & 1 & & 1 & 1 \\\text { C } & 1 & 1 & 1 & \\\text { D } & 1 & & & 1 \\\hline \text { COST }(\$ 000 \mathrm{~s}) & 200 & 150 & 190 & 250\end{array}$

$\text { MIN: } \quad 200 \mathrm{X}_{1}+150 \mathrm{X}_{2}+190 \mathrm{X}_{3}+250 \mathrm{X}_{4}$

$\text { Subject to:}$
$\begin{array}{l}\mathrm{X}_{2}+\mathrm{X}_{4} \geq 1 \\\mathrm{X}_{1}+\mathrm{X}_{3}+\mathrm{X}_{4} \geq 1 \\\mathrm{X}_{1}+\mathrm{X}_{2}+\mathrm{X}_{3} \geq 1 \\\mathrm{X}_{1}+\mathrm{X}_{4} \geq 1 \\\mathrm{X}_{1}+\mathrm{X}_{2}+\mathrm{X}_{3}+\mathrm{X}_{4}=2 \\\mathrm{X}_{\mathrm{i}}=0,1\end{array}$ Based on this ILP formulation of the problem what formulas should go in cells F6:F14 of the following Excel spreadsheet?