Essay
An investor is developing a portfolio of stocks. She has identified 3 stocks in which to invest. She wants to earn at least 11% return but with minimum risk.
Let: Pi = proportion of total funds invested in i, i = A, B, C
The NLP for this problem is:
MIN:
Subject to:
What formulas should go in cells G4:J14 of the spreadsheet for this problem? NOTE: Formulas are not required in all of these cells.
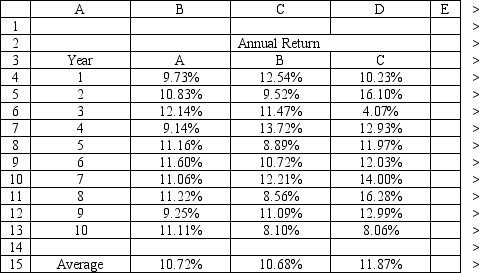
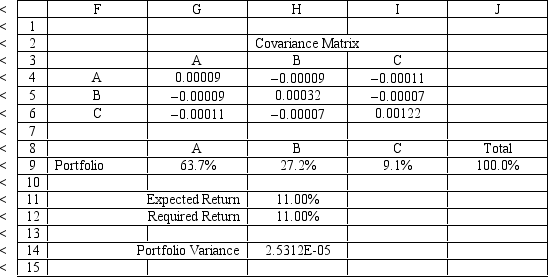
Correct Answer:

Verified
Correct Answer:
Verified
Q4: Exhibit 8.2<br>The following questions pertain to the
Q24: The straight line (Euclidean) distance between two
Q52: The total annual cost for the economic
Q59: An office supply company is attempting
Q60: An office supply company is attempting
Q63: A company wants to locate a
Q65: The optimal solution to a NLP problem
Q66: Project 8.1 - Truck Company Expansion<br>Kornfield
Q67: An investor is developing a portfolio of
Q68: How much must the objective function