The Owner of Fix-A-Dent Auto Repair Wants to Study the Growth

Multiple Choice

The owner of Fix-a-dent Auto Repair wants to study the growth of his business using simulation. He is interested in simulating the number of damaged cars and the amount of damage to the cars each month. He currently repairs 100 cars per month and feels this can vary uniformly between a decrease of as much as 3% and an increase of up to 5% (average change of 1%) over the previous months. The dollar value of the damage to the cars is a normally distributed random variable with a mean of $3,000 and a standard deviation of $500. The average repair bill has been increasing steadily over the years and the owner expects the mean repair bill will increase by 1% per month. You have created the following spreadsheet to simulate the problem.

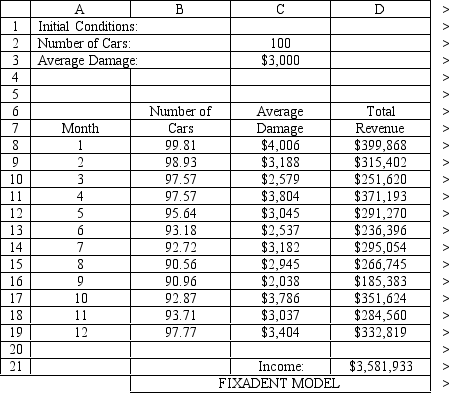
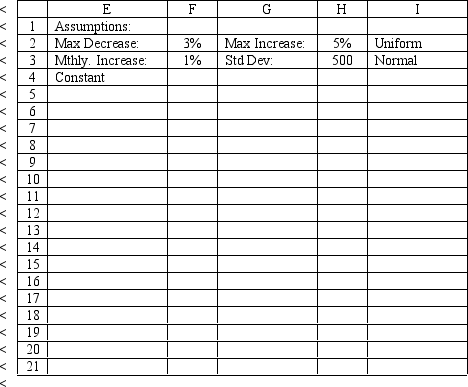
-Using the information in Exhibit 12.1, what Risk Solver Platform (RSP) function should go in cell C8 and copied to cells C9:C19 to compute the average damage per car in the month?

A) =PsiNormal($C$3*$F$3^$A$8, $H$3)
B) =PsiNormal($C$3*$F$3^A8, $H$3)
C) =PsiNormal($C$3, $D$3*(1+$F$3) ^A8)
D) =PsiNormal($C$3*(1+$F$3) ^A8, $H$3)