Essay
Project 12.1- Monte Carlo Integration
A common application of Monte Carlo simulation is to provide numerical approximations. One such application is to approximate the area under a curve, or Monte Carlo integration. The following figure represents such a curve, defined over the range of X = 0 to X = 13. Call the area under this curve A.
Monte Carlo integration begins by overlaying on the curve of interest a region (call this region, B) whose area is easy to calculate (i.e., a box). Monte Carlo integration then involves the random generation of points in B and a determination of the percentage of these points that fall in A (i.e., fall below the curve). This percentage represents that portion of the area of B that is the area of A.
Use Monte Carlo integration techniques to approximate the area under the curve. Use exact techniques to calculate the true area under the curve. How accurate is your approximation?
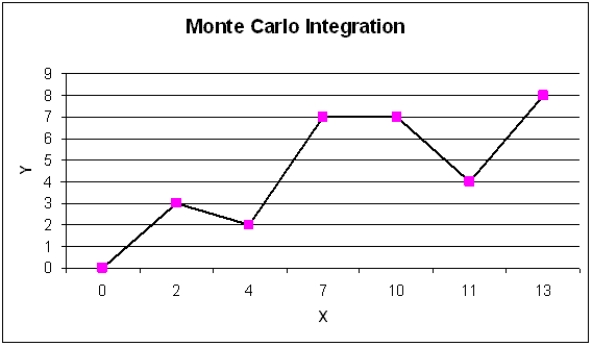
Correct Answer:

Verified
There are 6 line segments in the curve. ...View Answer
Unlock this answer now
Get Access to more Verified Answers free of charge
Correct Answer:
Verified
View Answer
Unlock this answer now
Get Access to more Verified Answers free of charge
Q5: A machine produces an average of
Q7: University Florists makes bouquets from a variety
Q8: An office supply store wants to simulate
Q11: <br>An auto parts store wants to simulate
Q51: <br>An auto parts store wants to simulate
Q54: Exhibit 12.3<br>The following questions use the information
Q55: Which of the following probability distributions are
Q56: <br>The owner of Fix-a-dent Auto Repair wants
Q62: <br>The owner of Fix-a-dent Auto Repair wants
Q66: Exhibit 12.4.<br>The following questions use the information