Multiple Choice
Select the correct graph of the given function.
A) 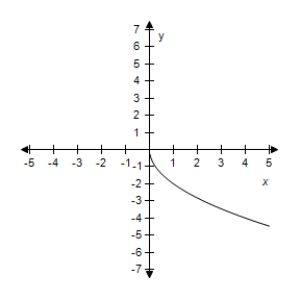
B) 
C) 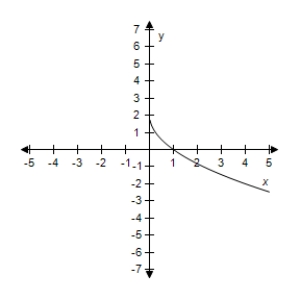
D) 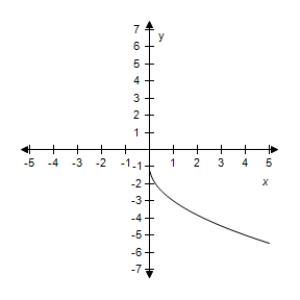
E) 
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q7: Find the coordinates of a second point
Q16: Evaluate g(s + 2)if g(y)= 12 -
Q230: Use the intercept form to find
Q231: Find the domain of the function.
Q232: Find the slope-intercept form of the
Q234: Determine whether the function has an
Q236: Assume that the graph has y-symmetry.Select the
Q238: Find <span class="ql-formula" data-value="f \circ
Q239: Find the inverse of the one-to-one
Q240: Graph the circle <span class="ql-formula"