Multiple Choice
Determine the intervals over which the function is increasing, decreasing, or constant. 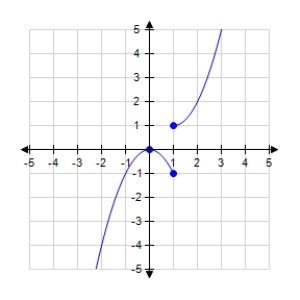
A) constant on (- , 0) increasing on (0, )
B) increasing on (- , 0) , (1, ) descreasing on (0, 1)
C) constant on (- , 1) increasing on (1, )
D) constant on (- , 1) descreasing on (1, )
E) constant on (- , 0) descreasing on (0, 1)
Correct Answer:

Verified
Correct Answer:
Verified
Q9: Determine the quadrant(s)in which (x,y)is located so
Q38: Find the coordinates of a second point
Q51: Find the midpoint between the two points
Q389: Find the slope of the line
Q391: Identify any intercepts and test for symmetry.Then
Q393: Find the slope and y-intercept (if
Q396: Use the graph of <span
Q397: Determine whether the function has an
Q398: Let <span class="ql-formula" data-value="f (
Q399: Assume that y is directly proportional