Multiple Choice
Use a graphing utility to graph the equation.Use the graph to approximate the values of x that satisfy each inequality.
Equation:
Inequality:
A) 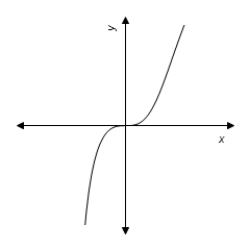
B) 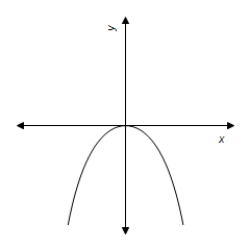
C) 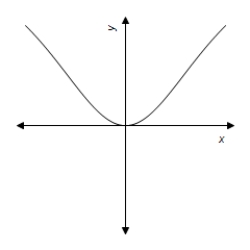
D) 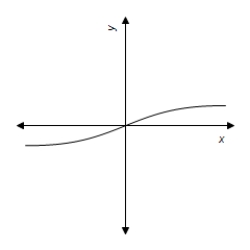
E) 
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q19: Find the key numbers of the
Q20: Use the Remainder Theorem and synthetic
Q23: The cost C (in millions of
Q25: Select the correct rational function for
Q26: Find the zeros of the rational
Q27: Determine the domain of <span
Q28: Select the correct graph of the
Q29: Find all the real zeros of
Q41: A manufacturer wants to enlarge an existing
Q47: Given 3 + i is a root,determine