Multiple Choice
Select the graph of and the transformation .
A) 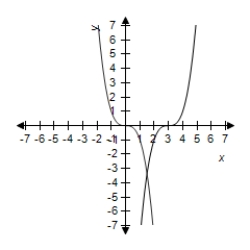
B) 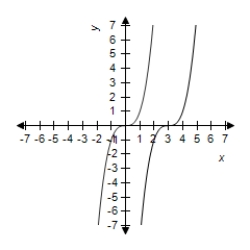
C) 
D) 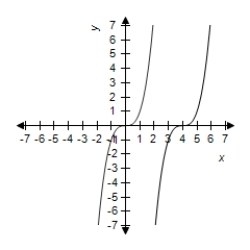
E) 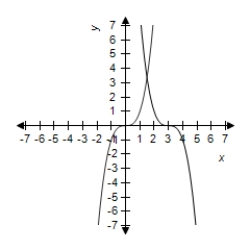
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q29: Find two positive real numbers whose product
Q368: Solve the inequality and write the
Q369: Select the correct graph of the
Q370: Find a polynomial with the given
Q371: Write the standard form of
Q372: Find domain of the following function.
Q374: Find all intercepts of the following
Q375: Determine the zeros (if any) of
Q376: Given <span class="ql-formula" data-value="f (
Q378: Find all the real zeros of