Multiple Choice
Select the graph of the function.
A) 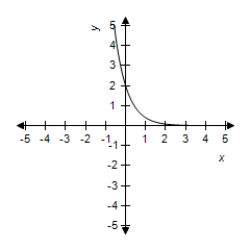
B) 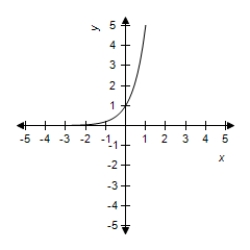
C) 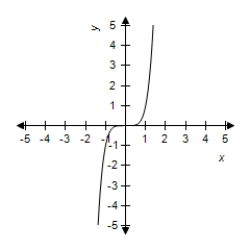
D) 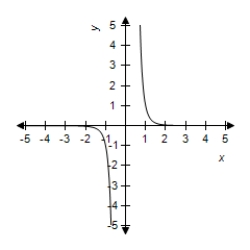
E) 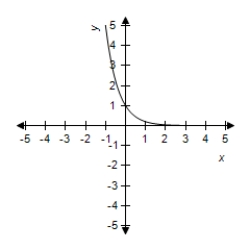
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q135: Rewrite the logarithm as a ratio
Q136: Write the logarithmic equation in exponential
Q137: Rewrite the logarithm as a ratio
Q138: Solve the logarithmic equation algebraically.Approximate the
Q139: Select the correct graph for the
Q141: Identify the value of the function
Q142: Condense the expression <span class="ql-formula"
Q143: Assume that x is a positive
Q144: Complete the table to determine the
Q145: Use the One-to-One Property to solve