Multiple Choice
Select the graph of the exponential function.
A) 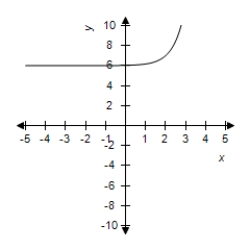
B) 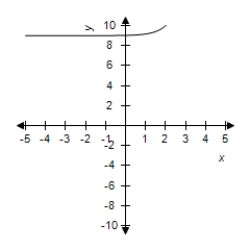
C) 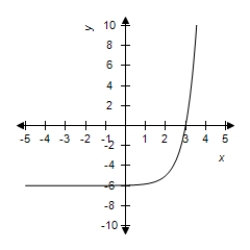
D) 
E) 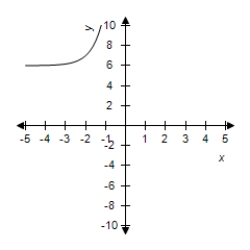
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q9: Simplify the expression log<sub>5</sub> 175.<br>A)35log<sub>5</sub> 2<br>B)2 log<sub>5</sub>
Q11: An initial investment of $4000 grows at
Q15: Solve the logarithmic equation algebraically.Approximate the
Q16: Evaluate <span class="ql-formula" data-value="f (
Q17: Rewrite the logarithmic equation <span
Q18: Determine whether or not <span
Q19: Evaluate the function at the indicated
Q21: Condense the expression to the logarithm
Q24: Carbon dating presumes that, as long
Q25: Write the logarithmic equation in exponential