Multiple Choice
Identify the graph of the function.
A) 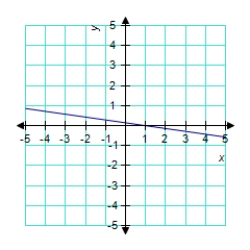
B) 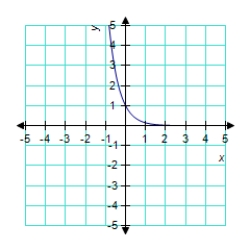
C) 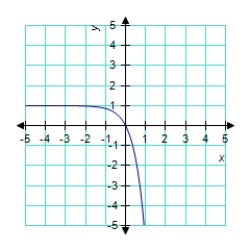
D) 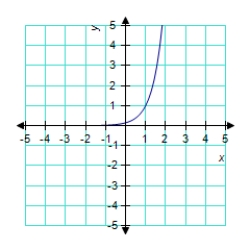
E) 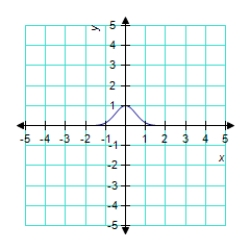
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q51: Find the exact value of the logarithmic
Q149: given that f(x) = ln x.<br><br>f(x -
Q157: Rewrite the logarithm as a ratio
Q158: Use the properties of logarithms to
Q159: Select the graph of the function.
Q160: Use a graphing utility to construct
Q161: Solve the exponential equation algebraically.Approximate the
Q164: Simplify the expression. <span
Q166: Write the logarithmic equation in exponential
Q167: Find the exponential model <span