The Linear Programming Problem Has an Unusual Characteristic

Multiple Choice

The linear programming problem has an unusual characteristic.Select a graph of the solution region for the problem and describe the unusual characteristic.Find the minimum and maximum value of the objective function (if possible) and where it occurs. ​
Z = x + y
​
Constraints:
​
X ≥ 0
Y ≥ 0
-x + y ≤ 0
-5x + y ≥ 5
​

A) 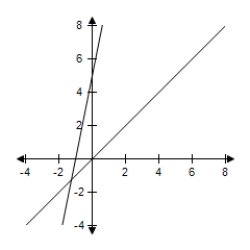Minimum at (0, 0) : 0Maximum at (-1,0) : -1
B) 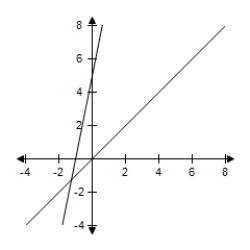Minimum at (0, 0) : 0Maximum at (0, 1) : 1
C) 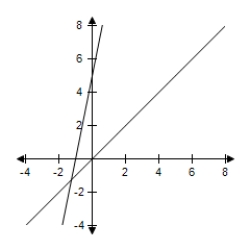Minimum at (-1, 0) : -1Maximum at (0, 0) : 0
D) 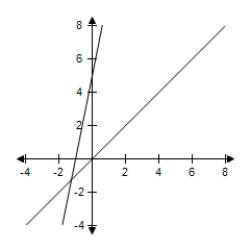Minimum at (0, 1) : 1Maximum at (0, 0) : 0
E) 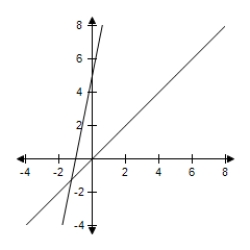The feasible set is empty.