The Linear Programming Problem Has an Unusual Characteristic

Multiple Choice

The linear programming problem has an unusual characteristic.Select a graph of the solution region for the problem and describe the unusual characteristic.Find the maximum value of the objective function (if possible) and where it occurs. ​
Z = 3x + 4y
​
Constraints:
​
X ≥ 0
Y ≥ 0
X + y ≤1
3x + y ≤ 6
​

A) ​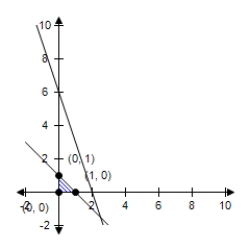 The constraint 3x + y ≤ 6 is extraneous. Maximum at (1, 1) : 7
B) ​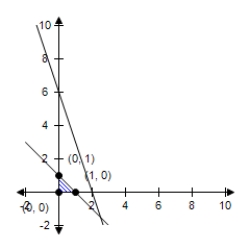 The constraint 3x + y ≤ 6 is extraneous. Maximum at (1, 0) : 3
C) ​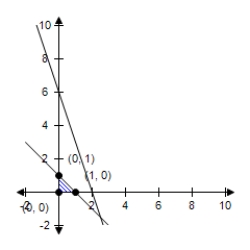 The constraint 3x + y ≤ 6 is extraneous. Maximum at (0, 1) : 4
D) ​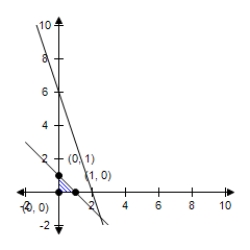 The constraint 3x + y ≤ 6 is extraneous. Maximum at (0, 0) : 0
E) ​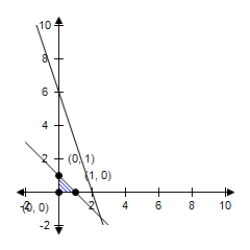 The constraint 3x + y ≤ 6 is extraneous. No maximum.