Solved

A Person Plans to Invest Up to $26,000 in Two {x+y=25,000y≥2xx≥5000y≥5000\left\{ \begin{array} { c } x + y = 25,000 \\y \geq 2 x \\x \geq 5000 \\y \geq 5000\end{array} \right.

Question 105

Multiple Choice

A person plans to invest up to $26,000 in two different interest-bearing accounts.Each account is to contain at least $5000.Moreover, the amount in one account should be at least twice the amount in the other account.Find and graph a system of inequalities to describe the various amounts that can be deposited in each account.


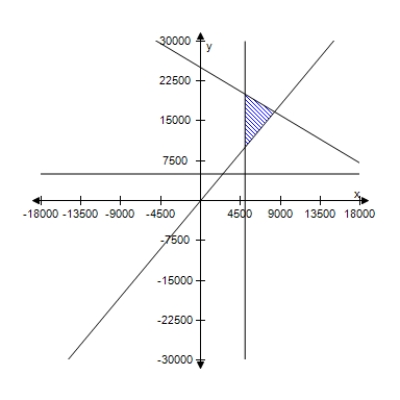
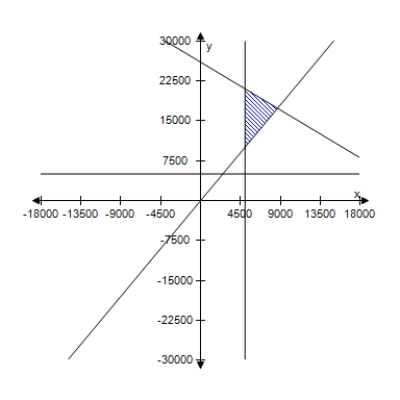
A) {x+y=25,000y≥2xx≥5000y≥5000\left\{ \begin{array} { c } x + y = 25,000 \\y \geq 2 x \\x \geq 5000 \\y \geq 5000\end{array} \right. A person plans to invest up to $26,000 in two different interest-bearing accounts.Each account is to contain at least $5000.Moreover, the amount in one account should be at least twice the amount in the other account.Find and graph a system of inequalities to describe the various amounts that can be deposited in each account. A) \left\{ \begin{array} { c } x + y = 25,000 \\ y \geq 2 x \\ x \geq 5000 \\ y \geq 5000 \end{array} \right. B) \left\{ \begin{array} { c } x + y \leq 26,000 \\ y \geq 2 x \\ x \geq 5000 \\ y \geq 5000 \end{array} \right. C) \left\{ \begin{array} { c } x + y = 22,000 \\ y \geq 2 x \\ x \geq 5000 \\ y \geq 5000 \end{array} \right. D) \left\{ \begin{array} { c } x + y \geq 30,000 \\ y \geq 2 x \\ x \geq 5000 \\ y \geq 5000 \end{array} \right. E) \left\{ \begin{array} { c } x + y \geq 23,000 \\ y \geq 2 x \\ x \geq 5000 \\ y \geq 5000 \end{array} \right.
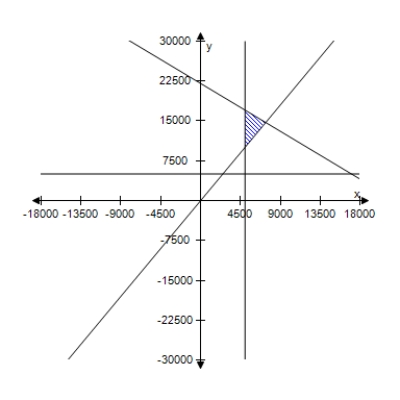
B) {x+y≤26,000y≥2xx≥5000y≥5000\left\{ \begin{array} { c } x + y \leq 26,000 \\y \geq 2 x \\x \geq 5000 \\y \geq 5000\end{array} \right. A person plans to invest up to $26,000 in two different interest-bearing accounts.Each account is to contain at least $5000.Moreover, the amount in one account should be at least twice the amount in the other account.Find and graph a system of inequalities to describe the various amounts that can be deposited in each account. A) \left\{ \begin{array} { c } x + y = 25,000 \\ y \geq 2 x \\ x \geq 5000 \\ y \geq 5000 \end{array} \right. B) \left\{ \begin{array} { c } x + y \leq 26,000 \\ y \geq 2 x \\ x \geq 5000 \\ y \geq 5000 \end{array} \right. C) \left\{ \begin{array} { c } x + y = 22,000 \\ y \geq 2 x \\ x \geq 5000 \\ y \geq 5000 \end{array} \right. D) \left\{ \begin{array} { c } x + y \geq 30,000 \\ y \geq 2 x \\ x \geq 5000 \\ y \geq 5000 \end{array} \right. E) \left\{ \begin{array} { c } x + y \geq 23,000 \\ y \geq 2 x \\ x \geq 5000 \\ y \geq 5000 \end{array} \right.
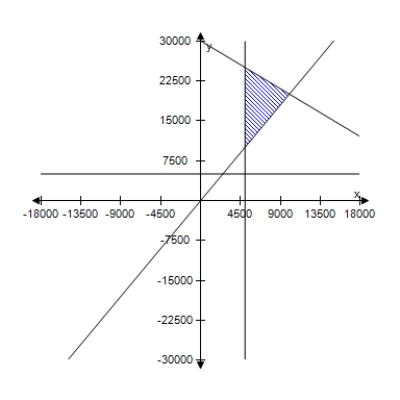
C) {x+y=22,000y≥2xx≥5000y≥5000\left\{ \begin{array} { c } x + y = 22,000 \\y \geq 2 x \\x \geq 5000 \\y \geq 5000\end{array} \right. A person plans to invest up to $26,000 in two different interest-bearing accounts.Each account is to contain at least $5000.Moreover, the amount in one account should be at least twice the amount in the other account.Find and graph a system of inequalities to describe the various amounts that can be deposited in each account. A) \left\{ \begin{array} { c } x + y = 25,000 \\ y \geq 2 x \\ x \geq 5000 \\ y \geq 5000 \end{array} \right. B) \left\{ \begin{array} { c } x + y \leq 26,000 \\ y \geq 2 x \\ x \geq 5000 \\ y \geq 5000 \end{array} \right. C) \left\{ \begin{array} { c } x + y = 22,000 \\ y \geq 2 x \\ x \geq 5000 \\ y \geq 5000 \end{array} \right. D) \left\{ \begin{array} { c } x + y \geq 30,000 \\ y \geq 2 x \\ x \geq 5000 \\ y \geq 5000 \end{array} \right. E) \left\{ \begin{array} { c } x + y \geq 23,000 \\ y \geq 2 x \\ x \geq 5000 \\ y \geq 5000 \end{array} \right.
D) {x+y≥30,000y≥2xx≥5000y≥5000\left\{ \begin{array} { c } x + y \geq 30,000 \\y \geq 2 x \\x \geq 5000 \\y \geq 5000\end{array} \right. A person plans to invest up to $26,000 in two different interest-bearing accounts.Each account is to contain at least $5000.Moreover, the amount in one account should be at least twice the amount in the other account.Find and graph a system of inequalities to describe the various amounts that can be deposited in each account. A) \left\{ \begin{array} { c } x + y = 25,000 \\ y \geq 2 x \\ x \geq 5000 \\ y \geq 5000 \end{array} \right. B) \left\{ \begin{array} { c } x + y \leq 26,000 \\ y \geq 2 x \\ x \geq 5000 \\ y \geq 5000 \end{array} \right. C) \left\{ \begin{array} { c } x + y = 22,000 \\ y \geq 2 x \\ x \geq 5000 \\ y \geq 5000 \end{array} \right. D) \left\{ \begin{array} { c } x + y \geq 30,000 \\ y \geq 2 x \\ x \geq 5000 \\ y \geq 5000 \end{array} \right. E) \left\{ \begin{array} { c } x + y \geq 23,000 \\ y \geq 2 x \\ x \geq 5000 \\ y \geq 5000 \end{array} \right.
E) {x+y≥23,000y≥2xx≥5000y≥5000\left\{ \begin{array} { c } x + y \geq 23,000 \\y \geq 2 x \\x \geq 5000 \\y \geq 5000\end{array} \right. A person plans to invest up to $26,000 in two different interest-bearing accounts.Each account is to contain at least $5000.Moreover, the amount in one account should be at least twice the amount in the other account.Find and graph a system of inequalities to describe the various amounts that can be deposited in each account. A) \left\{ \begin{array} { c } x + y = 25,000 \\ y \geq 2 x \\ x \geq 5000 \\ y \geq 5000 \end{array} \right. B) \left\{ \begin{array} { c } x + y \leq 26,000 \\ y \geq 2 x \\ x \geq 5000 \\ y \geq 5000 \end{array} \right. C) \left\{ \begin{array} { c } x + y = 22,000 \\ y \geq 2 x \\ x \geq 5000 \\ y \geq 5000 \end{array} \right. D) \left\{ \begin{array} { c } x + y \geq 30,000 \\ y \geq 2 x \\ x \geq 5000 \\ y \geq 5000 \end{array} \right. E) \left\{ \begin{array} { c } x + y \geq 23,000 \\ y \geq 2 x \\ x \geq 5000 \\ y \geq 5000 \end{array} \right.

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q34: Two cheeseburgers and one small order of

Q100: Find the minimum value of the

Q101: Solve the system by substitution, if

Q102: Sixty liters of a 43% acid

Q103: Find the value of x, y and

Q104: Solve the system by the method

Q107: Use any method to solve the

Q108: The linear programming problem has an unusual

Q109: Find the dimensions of the rectangle

Q110: Select the correct graph of the