Solved

For a Concert Event, There Are $30 Reserved Seat Tickets {x+y≤300030x+20y≥72,000x≤2000x≥0y≥0\left\{ \begin{array} { c } x + y \leq 3000 \\30 x + 20 y \geq 72,000 \\x \leq 2000 \\x \geq 0 \\y \geq 0\end{array} \right.

Question 82

Multiple Choice

For a concert event, there are $30 reserved seat tickets and $20 general admission tickets.There are 2000 reserved seats available, and fire regulations limit the number of paid ticket holders to 3000.The promoter must take in at least $65,000 in ticket sales.Find and graph a system of inequalities describing the different numbers of tickets that can be sold.


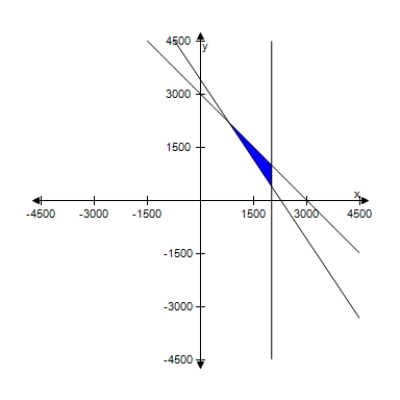
A) {x+y≤300030x+20y≥72,000x≤2000x≥0y≥0\left\{ \begin{array} { c } x + y \leq 3000 \\30 x + 20 y \geq 72,000 \\x \leq 2000 \\x \geq 0 \\y \geq 0\end{array} \right. For a concert event, there are $30 reserved seat tickets and $20 general admission tickets.There are 2000 reserved seats available, and fire regulations limit the number of paid ticket holders to 3000.The promoter must take in at least $65,000 in ticket sales.Find and graph a system of inequalities describing the different numbers of tickets that can be sold. A) \left\{ \begin{array} { c } x + y \leq 3000 \\ 30 x + 20 y \geq 72,000 \\ x \leq 2000 \\ x \geq 0 \\ y \geq 0 \end{array} \right. B) \left\{ \begin{array} { c } x + y \leq 3000 \\ 30 x + 20 y \geq 68,000 \\ x \leq 2000 \\ x \geq 0 \\ y \geq 0 \end{array} \right. C) \left\{ \begin{array} { c } x + y \leq 3000 \\ 30 x + 20 y \geq 66,000 \\ x \leq 2000 \\ x \geq 0 \\ y \geq 0 \end{array} \right. D) \left\{ \begin{array} { c } x + y \leq 3000 \\ 30 x + 20 y \geq 73,000 \\ x \leq 2000 \\ x \geq 0 \\ y \geq 0 \end{array} \right. E) \left\{ \begin{array} { c } x + y \leq 3000 \\ 30 x + 20 y \geq 65,000 \\ x \leq 2000 \\ x \geq 0 \\ y \geq 0 \end{array} \right.
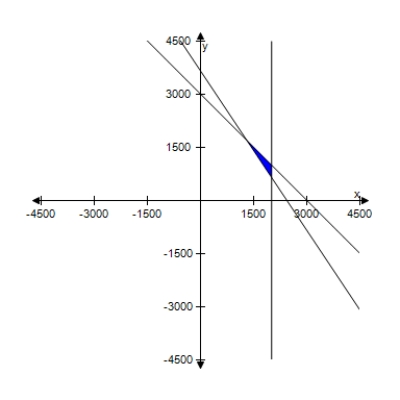
B) {x+y≤300030x+20y≥68,000x≤2000x≥0y≥0\left\{ \begin{array} { c } x + y \leq 3000 \\30 x + 20 y \geq 68,000 \\x \leq 2000 \\x \geq 0 \\y \geq 0\end{array} \right. For a concert event, there are $30 reserved seat tickets and $20 general admission tickets.There are 2000 reserved seats available, and fire regulations limit the number of paid ticket holders to 3000.The promoter must take in at least $65,000 in ticket sales.Find and graph a system of inequalities describing the different numbers of tickets that can be sold. A) \left\{ \begin{array} { c } x + y \leq 3000 \\ 30 x + 20 y \geq 72,000 \\ x \leq 2000 \\ x \geq 0 \\ y \geq 0 \end{array} \right. B) \left\{ \begin{array} { c } x + y \leq 3000 \\ 30 x + 20 y \geq 68,000 \\ x \leq 2000 \\ x \geq 0 \\ y \geq 0 \end{array} \right. C) \left\{ \begin{array} { c } x + y \leq 3000 \\ 30 x + 20 y \geq 66,000 \\ x \leq 2000 \\ x \geq 0 \\ y \geq 0 \end{array} \right. D) \left\{ \begin{array} { c } x + y \leq 3000 \\ 30 x + 20 y \geq 73,000 \\ x \leq 2000 \\ x \geq 0 \\ y \geq 0 \end{array} \right. E) \left\{ \begin{array} { c } x + y \leq 3000 \\ 30 x + 20 y \geq 65,000 \\ x \leq 2000 \\ x \geq 0 \\ y \geq 0 \end{array} \right.
C) {x+y≤300030x+20y≥66,000x≤2000x≥0y≥0\left\{ \begin{array} { c } x + y \leq 3000 \\30 x + 20 y \geq 66,000 \\x \leq 2000 \\x \geq 0 \\y \geq 0\end{array} \right. For a concert event, there are $30 reserved seat tickets and $20 general admission tickets.There are 2000 reserved seats available, and fire regulations limit the number of paid ticket holders to 3000.The promoter must take in at least $65,000 in ticket sales.Find and graph a system of inequalities describing the different numbers of tickets that can be sold. A) \left\{ \begin{array} { c } x + y \leq 3000 \\ 30 x + 20 y \geq 72,000 \\ x \leq 2000 \\ x \geq 0 \\ y \geq 0 \end{array} \right. B) \left\{ \begin{array} { c } x + y \leq 3000 \\ 30 x + 20 y \geq 68,000 \\ x \leq 2000 \\ x \geq 0 \\ y \geq 0 \end{array} \right. C) \left\{ \begin{array} { c } x + y \leq 3000 \\ 30 x + 20 y \geq 66,000 \\ x \leq 2000 \\ x \geq 0 \\ y \geq 0 \end{array} \right. D) \left\{ \begin{array} { c } x + y \leq 3000 \\ 30 x + 20 y \geq 73,000 \\ x \leq 2000 \\ x \geq 0 \\ y \geq 0 \end{array} \right. E) \left\{ \begin{array} { c } x + y \leq 3000 \\ 30 x + 20 y \geq 65,000 \\ x \leq 2000 \\ x \geq 0 \\ y \geq 0 \end{array} \right.
D) {x+y≤300030x+20y≥73,000x≤2000x≥0y≥0\left\{ \begin{array} { c } x + y \leq 3000 \\30 x + 20 y \geq 73,000 \\x \leq 2000 \\x \geq 0 \\y \geq 0\end{array} \right. For a concert event, there are $30 reserved seat tickets and $20 general admission tickets.There are 2000 reserved seats available, and fire regulations limit the number of paid ticket holders to 3000.The promoter must take in at least $65,000 in ticket sales.Find and graph a system of inequalities describing the different numbers of tickets that can be sold. A) \left\{ \begin{array} { c } x + y \leq 3000 \\ 30 x + 20 y \geq 72,000 \\ x \leq 2000 \\ x \geq 0 \\ y \geq 0 \end{array} \right. B) \left\{ \begin{array} { c } x + y \leq 3000 \\ 30 x + 20 y \geq 68,000 \\ x \leq 2000 \\ x \geq 0 \\ y \geq 0 \end{array} \right. C) \left\{ \begin{array} { c } x + y \leq 3000 \\ 30 x + 20 y \geq 66,000 \\ x \leq 2000 \\ x \geq 0 \\ y \geq 0 \end{array} \right. D) \left\{ \begin{array} { c } x + y \leq 3000 \\ 30 x + 20 y \geq 73,000 \\ x \leq 2000 \\ x \geq 0 \\ y \geq 0 \end{array} \right. E) \left\{ \begin{array} { c } x + y \leq 3000 \\ 30 x + 20 y \geq 65,000 \\ x \leq 2000 \\ x \geq 0 \\ y \geq 0 \end{array} \right.
E) {x+y≤300030x+20y≥65,000x≤2000x≥0y≥0\left\{ \begin{array} { c } x + y \leq 3000 \\30 x + 20 y \geq 65,000 \\x \leq 2000 \\x \geq 0 \\y \geq 0\end{array} \right. For a concert event, there are $30 reserved seat tickets and $20 general admission tickets.There are 2000 reserved seats available, and fire regulations limit the number of paid ticket holders to 3000.The promoter must take in at least $65,000 in ticket sales.Find and graph a system of inequalities describing the different numbers of tickets that can be sold. A) \left\{ \begin{array} { c } x + y \leq 3000 \\ 30 x + 20 y \geq 72,000 \\ x \leq 2000 \\ x \geq 0 \\ y \geq 0 \end{array} \right. B) \left\{ \begin{array} { c } x + y \leq 3000 \\ 30 x + 20 y \geq 68,000 \\ x \leq 2000 \\ x \geq 0 \\ y \geq 0 \end{array} \right. C) \left\{ \begin{array} { c } x + y \leq 3000 \\ 30 x + 20 y \geq 66,000 \\ x \leq 2000 \\ x \geq 0 \\ y \geq 0 \end{array} \right. D) \left\{ \begin{array} { c } x + y \leq 3000 \\ 30 x + 20 y \geq 73,000 \\ x \leq 2000 \\ x \geq 0 \\ y \geq 0 \end{array} \right. E) \left\{ \begin{array} { c } x + y \leq 3000 \\ 30 x + 20 y \geq 65,000 \\ x \leq 2000 \\ x \geq 0 \\ y \geq 0 \end{array} \right.

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q29: An animal shelter mixes two brands of

Q77: Find the consumer surplus and producer

Q78: Determine which one of the ordered

Q79: Solve the system by the method

Q80: A dietitian is asked to design

Q81: Use a graphing utility to solve

Q83: Solve the system of linear equations

Q84: Write the form of the partial

Q85: Find the minimum value of the objective

Q87: Find the maximum value of the