Solved

Select the Correct Graph of the Polar Equation r=8sin⁡θcos⁡2θr = 8 \sin \theta \cos ^ { 2 } \theta

Question 252

Multiple Choice

Select the correct graph of the polar equation.Describe your viewing window. r=8sin⁡θcos⁡2θr = 8 \sin \theta \cos ^ { 2 } \theta


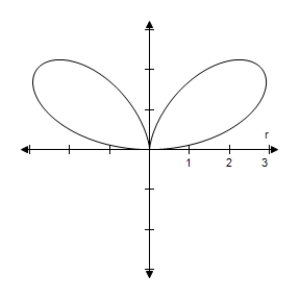
A) Select the correct graph of the polar equation.Describe your viewing window. r = 8 \sin \theta \cos ^ { 2 } \theta A) \begin{array} { l } \theta _ { \min } = 0 \\ \theta _ { \max } = 2 \pi \\ \theta _ { s t e p } = \pi / 24 \\ X _ { \min } = - 3 \\ X _ { \max } = 3 \\ X _ { s c l } = 1 \\ Y _ { \min } = - 3 \\ Y _ { \max } = 3 \\ Y _ { s c l } = 1 \end{array} B) \begin{array} { l } \theta _ { \min } = 0 \\ \theta _ { \max } = 2 \pi \\ \theta _ { s t e p } = \pi / 24 \\ X _ { \min } = - 3 \\ X _ { \max } = 3 \\ X _ { s c l } = 1 \\ Y _ { \min } = - 3 \\ Y _ { \max } = 3 \\ Y _ { s c l } = 1 \end{array} C) \begin{array} { l } \theta _ { \min } = 0 \\ \theta _ { \max } = 2 \pi \\ \theta _ { s t e p } = \pi / 24 \\ X _ { \min } = - 3 \\ X _ { \max } = 3 \\ X _ { s c l } = 1 \\ Y _ { \min } = - 3 \\ Y _ { \max } = 3 \\ Y _ { s c l } = 1 \end{array} D) \begin{array} { l } \theta _ { \min } = 0 \\ \theta _ { \max } = 2 \pi \\ \theta _ { s t e p } = \pi / 24 \\ X _ { \min } = - 3 \\ X _ { \max } = 3 \\ X _ { s c l } = 1 \\ Y _ { \min } = - 3 \\ Y _ { \max } = 3 \\ Y _ { s c l } = 1 \end{array} E) \begin{array} { l } \theta _ { \min } = 0 \\ \theta _ { \max } = 2 \pi \\ \theta _ { s t e p } = \pi / 24 \\ X _ { \min } = - 3 \\ X _ { \max } = 3 \\ X _ { s c l } = 1 \\ Y _ { \min } = - 3 \\ Y _ { \max } = 3 \\ Y _ { s c l } = 1 \end{array} θmin⁡=0θmax⁡=2πθstep=π/24Xmin⁡=−3Xmax⁡=3Xscl=1Ymin⁡=−3Ymax⁡=3Yscl=1\begin{array} { l } \theta _ { \min } = 0 \\\theta _ { \max } = 2 \pi \\\theta _ { s t e p } = \pi / 24 \\X _ { \min } = - 3 \\X _ { \max } = 3 \\X _ { s c l } = 1 \\Y _ { \min } = - 3 \\Y _ { \max } = 3 \\Y _ { s c l } = 1\end{array}
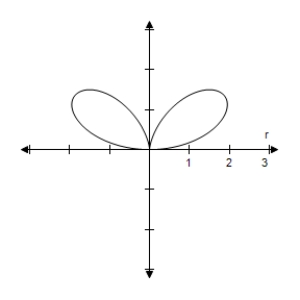
B) Select the correct graph of the polar equation.Describe your viewing window. r = 8 \sin \theta \cos ^ { 2 } \theta A) \begin{array} { l } \theta _ { \min } = 0 \\ \theta _ { \max } = 2 \pi \\ \theta _ { s t e p } = \pi / 24 \\ X _ { \min } = - 3 \\ X _ { \max } = 3 \\ X _ { s c l } = 1 \\ Y _ { \min } = - 3 \\ Y _ { \max } = 3 \\ Y _ { s c l } = 1 \end{array} B) \begin{array} { l } \theta _ { \min } = 0 \\ \theta _ { \max } = 2 \pi \\ \theta _ { s t e p } = \pi / 24 \\ X _ { \min } = - 3 \\ X _ { \max } = 3 \\ X _ { s c l } = 1 \\ Y _ { \min } = - 3 \\ Y _ { \max } = 3 \\ Y _ { s c l } = 1 \end{array} C) \begin{array} { l } \theta _ { \min } = 0 \\ \theta _ { \max } = 2 \pi \\ \theta _ { s t e p } = \pi / 24 \\ X _ { \min } = - 3 \\ X _ { \max } = 3 \\ X _ { s c l } = 1 \\ Y _ { \min } = - 3 \\ Y _ { \max } = 3 \\ Y _ { s c l } = 1 \end{array} D) \begin{array} { l } \theta _ { \min } = 0 \\ \theta _ { \max } = 2 \pi \\ \theta _ { s t e p } = \pi / 24 \\ X _ { \min } = - 3 \\ X _ { \max } = 3 \\ X _ { s c l } = 1 \\ Y _ { \min } = - 3 \\ Y _ { \max } = 3 \\ Y _ { s c l } = 1 \end{array} E) \begin{array} { l } \theta _ { \min } = 0 \\ \theta _ { \max } = 2 \pi \\ \theta _ { s t e p } = \pi / 24 \\ X _ { \min } = - 3 \\ X _ { \max } = 3 \\ X _ { s c l } = 1 \\ Y _ { \min } = - 3 \\ Y _ { \max } = 3 \\ Y _ { s c l } = 1 \end{array} θmin⁡=0θmax⁡=2πθstep=π/24Xmin⁡=−3Xmax⁡=3Xscl=1Ymin⁡=−3Ymax⁡=3Yscl=1\begin{array} { l } \theta _ { \min } = 0 \\\theta _ { \max } = 2 \pi \\\theta _ { s t e p } = \pi / 24 \\X _ { \min } = - 3 \\X _ { \max } = 3 \\X _ { s c l } = 1 \\Y _ { \min } = - 3 \\Y _ { \max } = 3 \\Y _ { s c l } = 1\end{array}
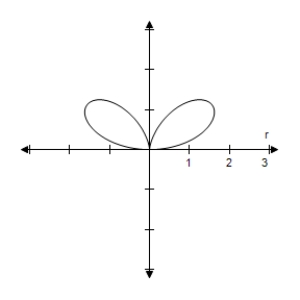
C) Select the correct graph of the polar equation.Describe your viewing window. r = 8 \sin \theta \cos ^ { 2 } \theta A) \begin{array} { l } \theta _ { \min } = 0 \\ \theta _ { \max } = 2 \pi \\ \theta _ { s t e p } = \pi / 24 \\ X _ { \min } = - 3 \\ X _ { \max } = 3 \\ X _ { s c l } = 1 \\ Y _ { \min } = - 3 \\ Y _ { \max } = 3 \\ Y _ { s c l } = 1 \end{array} B) \begin{array} { l } \theta _ { \min } = 0 \\ \theta _ { \max } = 2 \pi \\ \theta _ { s t e p } = \pi / 24 \\ X _ { \min } = - 3 \\ X _ { \max } = 3 \\ X _ { s c l } = 1 \\ Y _ { \min } = - 3 \\ Y _ { \max } = 3 \\ Y _ { s c l } = 1 \end{array} C) \begin{array} { l } \theta _ { \min } = 0 \\ \theta _ { \max } = 2 \pi \\ \theta _ { s t e p } = \pi / 24 \\ X _ { \min } = - 3 \\ X _ { \max } = 3 \\ X _ { s c l } = 1 \\ Y _ { \min } = - 3 \\ Y _ { \max } = 3 \\ Y _ { s c l } = 1 \end{array} D) \begin{array} { l } \theta _ { \min } = 0 \\ \theta _ { \max } = 2 \pi \\ \theta _ { s t e p } = \pi / 24 \\ X _ { \min } = - 3 \\ X _ { \max } = 3 \\ X _ { s c l } = 1 \\ Y _ { \min } = - 3 \\ Y _ { \max } = 3 \\ Y _ { s c l } = 1 \end{array} E) \begin{array} { l } \theta _ { \min } = 0 \\ \theta _ { \max } = 2 \pi \\ \theta _ { s t e p } = \pi / 24 \\ X _ { \min } = - 3 \\ X _ { \max } = 3 \\ X _ { s c l } = 1 \\ Y _ { \min } = - 3 \\ Y _ { \max } = 3 \\ Y _ { s c l } = 1 \end{array} θmin⁡=0θmax⁡=2πθstep=π/24Xmin⁡=−3Xmax⁡=3Xscl=1Ymin⁡=−3Ymax⁡=3Yscl=1\begin{array} { l } \theta _ { \min } = 0 \\\theta _ { \max } = 2 \pi \\\theta _ { s t e p } = \pi / 24 \\X _ { \min } = - 3 \\X _ { \max } = 3 \\X _ { s c l } = 1 \\Y _ { \min } = - 3 \\Y _ { \max } = 3 \\Y _ { s c l } = 1\end{array}
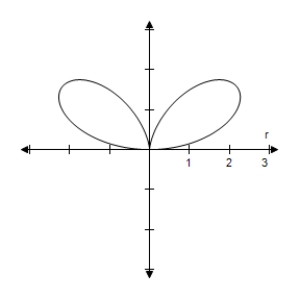
D) Select the correct graph of the polar equation.Describe your viewing window. r = 8 \sin \theta \cos ^ { 2 } \theta A) \begin{array} { l } \theta _ { \min } = 0 \\ \theta _ { \max } = 2 \pi \\ \theta _ { s t e p } = \pi / 24 \\ X _ { \min } = - 3 \\ X _ { \max } = 3 \\ X _ { s c l } = 1 \\ Y _ { \min } = - 3 \\ Y _ { \max } = 3 \\ Y _ { s c l } = 1 \end{array} B) \begin{array} { l } \theta _ { \min } = 0 \\ \theta _ { \max } = 2 \pi \\ \theta _ { s t e p } = \pi / 24 \\ X _ { \min } = - 3 \\ X _ { \max } = 3 \\ X _ { s c l } = 1 \\ Y _ { \min } = - 3 \\ Y _ { \max } = 3 \\ Y _ { s c l } = 1 \end{array} C) \begin{array} { l } \theta _ { \min } = 0 \\ \theta _ { \max } = 2 \pi \\ \theta _ { s t e p } = \pi / 24 \\ X _ { \min } = - 3 \\ X _ { \max } = 3 \\ X _ { s c l } = 1 \\ Y _ { \min } = - 3 \\ Y _ { \max } = 3 \\ Y _ { s c l } = 1 \end{array} D) \begin{array} { l } \theta _ { \min } = 0 \\ \theta _ { \max } = 2 \pi \\ \theta _ { s t e p } = \pi / 24 \\ X _ { \min } = - 3 \\ X _ { \max } = 3 \\ X _ { s c l } = 1 \\ Y _ { \min } = - 3 \\ Y _ { \max } = 3 \\ Y _ { s c l } = 1 \end{array} E) \begin{array} { l } \theta _ { \min } = 0 \\ \theta _ { \max } = 2 \pi \\ \theta _ { s t e p } = \pi / 24 \\ X _ { \min } = - 3 \\ X _ { \max } = 3 \\ X _ { s c l } = 1 \\ Y _ { \min } = - 3 \\ Y _ { \max } = 3 \\ Y _ { s c l } = 1 \end{array} θmin⁡=0θmax⁡=2πθstep=π/24Xmin⁡=−3Xmax⁡=3Xscl=1Ymin⁡=−3Ymax⁡=3Yscl=1\begin{array} { l } \theta _ { \min } = 0 \\\theta _ { \max } = 2 \pi \\\theta _ { s t e p } = \pi / 24 \\X _ { \min } = - 3 \\X _ { \max } = 3 \\X _ { s c l } = 1 \\Y _ { \min } = - 3 \\Y _ { \max } = 3 \\Y _ { s c l } = 1\end{array}
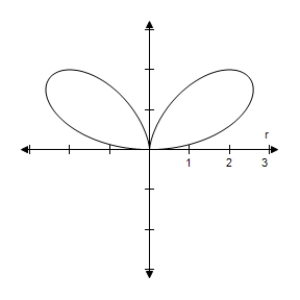
E) Select the correct graph of the polar equation.Describe your viewing window. r = 8 \sin \theta \cos ^ { 2 } \theta A) \begin{array} { l } \theta _ { \min } = 0 \\ \theta _ { \max } = 2 \pi \\ \theta _ { s t e p } = \pi / 24 \\ X _ { \min } = - 3 \\ X _ { \max } = 3 \\ X _ { s c l } = 1 \\ Y _ { \min } = - 3 \\ Y _ { \max } = 3 \\ Y _ { s c l } = 1 \end{array} B) \begin{array} { l } \theta _ { \min } = 0 \\ \theta _ { \max } = 2 \pi \\ \theta _ { s t e p } = \pi / 24 \\ X _ { \min } = - 3 \\ X _ { \max } = 3 \\ X _ { s c l } = 1 \\ Y _ { \min } = - 3 \\ Y _ { \max } = 3 \\ Y _ { s c l } = 1 \end{array} C) \begin{array} { l } \theta _ { \min } = 0 \\ \theta _ { \max } = 2 \pi \\ \theta _ { s t e p } = \pi / 24 \\ X _ { \min } = - 3 \\ X _ { \max } = 3 \\ X _ { s c l } = 1 \\ Y _ { \min } = - 3 \\ Y _ { \max } = 3 \\ Y _ { s c l } = 1 \end{array} D) \begin{array} { l } \theta _ { \min } = 0 \\ \theta _ { \max } = 2 \pi \\ \theta _ { s t e p } = \pi / 24 \\ X _ { \min } = - 3 \\ X _ { \max } = 3 \\ X _ { s c l } = 1 \\ Y _ { \min } = - 3 \\ Y _ { \max } = 3 \\ Y _ { s c l } = 1 \end{array} E) \begin{array} { l } \theta _ { \min } = 0 \\ \theta _ { \max } = 2 \pi \\ \theta _ { s t e p } = \pi / 24 \\ X _ { \min } = - 3 \\ X _ { \max } = 3 \\ X _ { s c l } = 1 \\ Y _ { \min } = - 3 \\ Y _ { \max } = 3 \\ Y _ { s c l } = 1 \end{array} θmin⁡=0θmax⁡=2πθstep=π/24Xmin⁡=−3Xmax⁡=3Xscl=1Ymin⁡=−3Ymax⁡=3Yscl=1\begin{array} { l } \theta _ { \min } = 0 \\\theta _ { \max } = 2 \pi \\\theta _ { s t e p } = \pi / 24 \\X _ { \min } = - 3 \\X _ { \max } = 3 \\X _ { s c l } = 1 \\Y _ { \min } = - 3 \\Y _ { \max } = 3 \\Y _ { s c l } = 1\end{array}

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q247: Convert the rectangular equation to polar

Q248: Use a graphing utility to graph

Q249: Select the correct graph of the

Q250: Find the standard form of the

Q251: Select the curve represented by the

Q253: Identify the conic as a circle

Q254: Select the correct graph of the

Q255: Find the standard form of the

Q256: Select the correct equation of the

Q257: Find the standard form of the