Solved

Select the Correct Graph of the Polar Equation r=2csc⁡θ+5r = 2 \csc \theta + 5

Question 546

Multiple Choice

Select the correct graph of the polar equation.Describe your viewing window. r=2csc⁡θ+5r = 2 \csc \theta + 5


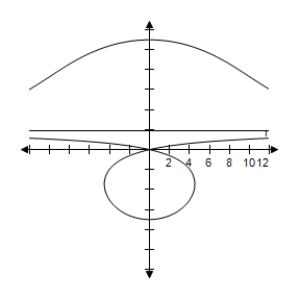
A) Select the correct graph of the polar equation.Describe your viewing window. r = 2 \csc \theta + 5 A) \begin{array} { l } \theta _ { \min } = 0 \\ \theta _ { \max } = 2 \pi \\ \theta _ { s t e p } = \pi / 24 \\ X _ { \min } = - 12 \\ X _ { \max } = 12 \\ X _ { s c l } = 2 \\ Y _ { \min } = - 12 \\ Y _ { \max } = 12 \\ Y _ { s c l } = 2 \end{array} B) \begin{array} { l } \theta _ { \min } = 0 \\ \theta _ { \max } = 2 \pi \\ \theta _ { s t e p } = \pi / 24 \\ X _ { \min } = - 12 \\ X _ { \max } = 12 \\ X _ { s c l } = 2 \\ Y _ { \min } = - 12 \\ Y _ { \max } = 12 \\ Y _ { s c l } = 2 \end{array} C) \begin{array} { l } \theta _ { \min } = 0 \\ \theta _ { \max } = 2 \pi \\ \theta _ { s t e p } = \pi / 24 \\ X _ { \min } = - 12 \\ X _ { \max } = 12 \\ X _ { s c l } = 2 \\ Y _ { \min } = - 12 \\ Y _ { \max } = 12 \\ Y _ { s c l } = 2 \end{array} D) \begin{array} { l } \theta _ { \min } = 0 \\ \theta _ { \max } = 2 \pi \\ \theta _ { s t e p } = \pi / 24 \\ X _ { \min } = - 12 \\ X _ { \max } = 12 \\ X _ { s c l } = 2 \\ Y _ { \min } = - 12 \\ Y _ { \max } = 12 \\ Y _ { s c l } = 2 \end{array} E) \begin{array} { l } \theta _ { \min } = 0 \\ \theta _ { \max } = 2 \pi \\ \theta _ { s t e p } = \pi / 24 \\ X _ { \min } = - 12 \\ X _ { \max } = 12 \\ X _ { s c l } = 2 \\ Y _ { \min } = - 12 \\ Y _ { \max } = 12 \\ Y _ { s c l } = 2 \end{array} θmin⁡=0θmax⁡=2πθstep=π/24Xmin⁡=−12Xmax⁡=12Xscl=2Ymin⁡=−12Ymax⁡=12Yscl=2\begin{array} { l } \theta _ { \min } = 0 \\\theta _ { \max } = 2 \pi \\\theta _ { s t e p } = \pi / 24 \\X _ { \min } = - 12 \\X _ { \max } = 12 \\X _ { s c l } = 2 \\Y _ { \min } = - 12 \\Y _ { \max } = 12 \\Y _ { s c l } = 2\end{array}
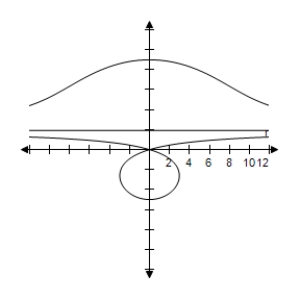
B) Select the correct graph of the polar equation.Describe your viewing window. r = 2 \csc \theta + 5 A) \begin{array} { l } \theta _ { \min } = 0 \\ \theta _ { \max } = 2 \pi \\ \theta _ { s t e p } = \pi / 24 \\ X _ { \min } = - 12 \\ X _ { \max } = 12 \\ X _ { s c l } = 2 \\ Y _ { \min } = - 12 \\ Y _ { \max } = 12 \\ Y _ { s c l } = 2 \end{array} B) \begin{array} { l } \theta _ { \min } = 0 \\ \theta _ { \max } = 2 \pi \\ \theta _ { s t e p } = \pi / 24 \\ X _ { \min } = - 12 \\ X _ { \max } = 12 \\ X _ { s c l } = 2 \\ Y _ { \min } = - 12 \\ Y _ { \max } = 12 \\ Y _ { s c l } = 2 \end{array} C) \begin{array} { l } \theta _ { \min } = 0 \\ \theta _ { \max } = 2 \pi \\ \theta _ { s t e p } = \pi / 24 \\ X _ { \min } = - 12 \\ X _ { \max } = 12 \\ X _ { s c l } = 2 \\ Y _ { \min } = - 12 \\ Y _ { \max } = 12 \\ Y _ { s c l } = 2 \end{array} D) \begin{array} { l } \theta _ { \min } = 0 \\ \theta _ { \max } = 2 \pi \\ \theta _ { s t e p } = \pi / 24 \\ X _ { \min } = - 12 \\ X _ { \max } = 12 \\ X _ { s c l } = 2 \\ Y _ { \min } = - 12 \\ Y _ { \max } = 12 \\ Y _ { s c l } = 2 \end{array} E) \begin{array} { l } \theta _ { \min } = 0 \\ \theta _ { \max } = 2 \pi \\ \theta _ { s t e p } = \pi / 24 \\ X _ { \min } = - 12 \\ X _ { \max } = 12 \\ X _ { s c l } = 2 \\ Y _ { \min } = - 12 \\ Y _ { \max } = 12 \\ Y _ { s c l } = 2 \end{array} θmin⁡=0θmax⁡=2πθstep=π/24Xmin⁡=−12Xmax⁡=12Xscl=2Ymin⁡=−12Ymax⁡=12Yscl=2\begin{array} { l } \theta _ { \min } = 0 \\\theta _ { \max } = 2 \pi \\\theta _ { s t e p } = \pi / 24 \\X _ { \min } = - 12 \\X _ { \max } = 12 \\X _ { s c l } = 2 \\Y _ { \min } = - 12 \\Y _ { \max } = 12 \\Y _ { s c l } = 2\end{array}
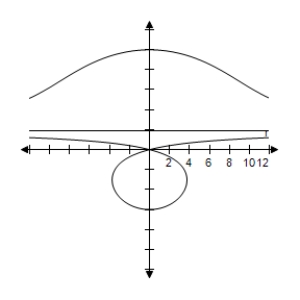
C) Select the correct graph of the polar equation.Describe your viewing window. r = 2 \csc \theta + 5 A) \begin{array} { l } \theta _ { \min } = 0 \\ \theta _ { \max } = 2 \pi \\ \theta _ { s t e p } = \pi / 24 \\ X _ { \min } = - 12 \\ X _ { \max } = 12 \\ X _ { s c l } = 2 \\ Y _ { \min } = - 12 \\ Y _ { \max } = 12 \\ Y _ { s c l } = 2 \end{array} B) \begin{array} { l } \theta _ { \min } = 0 \\ \theta _ { \max } = 2 \pi \\ \theta _ { s t e p } = \pi / 24 \\ X _ { \min } = - 12 \\ X _ { \max } = 12 \\ X _ { s c l } = 2 \\ Y _ { \min } = - 12 \\ Y _ { \max } = 12 \\ Y _ { s c l } = 2 \end{array} C) \begin{array} { l } \theta _ { \min } = 0 \\ \theta _ { \max } = 2 \pi \\ \theta _ { s t e p } = \pi / 24 \\ X _ { \min } = - 12 \\ X _ { \max } = 12 \\ X _ { s c l } = 2 \\ Y _ { \min } = - 12 \\ Y _ { \max } = 12 \\ Y _ { s c l } = 2 \end{array} D) \begin{array} { l } \theta _ { \min } = 0 \\ \theta _ { \max } = 2 \pi \\ \theta _ { s t e p } = \pi / 24 \\ X _ { \min } = - 12 \\ X _ { \max } = 12 \\ X _ { s c l } = 2 \\ Y _ { \min } = - 12 \\ Y _ { \max } = 12 \\ Y _ { s c l } = 2 \end{array} E) \begin{array} { l } \theta _ { \min } = 0 \\ \theta _ { \max } = 2 \pi \\ \theta _ { s t e p } = \pi / 24 \\ X _ { \min } = - 12 \\ X _ { \max } = 12 \\ X _ { s c l } = 2 \\ Y _ { \min } = - 12 \\ Y _ { \max } = 12 \\ Y _ { s c l } = 2 \end{array} θmin⁡=0θmax⁡=2πθstep=π/24Xmin⁡=−12Xmax⁡=12Xscl=2Ymin⁡=−12Ymax⁡=12Yscl=2\begin{array} { l } \theta _ { \min } = 0 \\\theta _ { \max } = 2 \pi \\\theta _ { s t e p } = \pi / 24 \\X _ { \min } = - 12 \\X _ { \max } = 12 \\X _ { s c l } = 2 \\Y _ { \min } = - 12 \\Y _ { \max } = 12 \\Y _ { s c l } = 2\end{array}
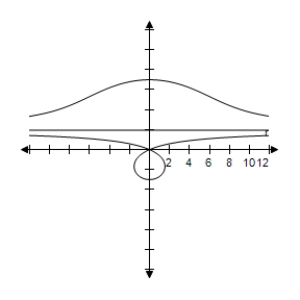
D) Select the correct graph of the polar equation.Describe your viewing window. r = 2 \csc \theta + 5 A) \begin{array} { l } \theta _ { \min } = 0 \\ \theta _ { \max } = 2 \pi \\ \theta _ { s t e p } = \pi / 24 \\ X _ { \min } = - 12 \\ X _ { \max } = 12 \\ X _ { s c l } = 2 \\ Y _ { \min } = - 12 \\ Y _ { \max } = 12 \\ Y _ { s c l } = 2 \end{array} B) \begin{array} { l } \theta _ { \min } = 0 \\ \theta _ { \max } = 2 \pi \\ \theta _ { s t e p } = \pi / 24 \\ X _ { \min } = - 12 \\ X _ { \max } = 12 \\ X _ { s c l } = 2 \\ Y _ { \min } = - 12 \\ Y _ { \max } = 12 \\ Y _ { s c l } = 2 \end{array} C) \begin{array} { l } \theta _ { \min } = 0 \\ \theta _ { \max } = 2 \pi \\ \theta _ { s t e p } = \pi / 24 \\ X _ { \min } = - 12 \\ X _ { \max } = 12 \\ X _ { s c l } = 2 \\ Y _ { \min } = - 12 \\ Y _ { \max } = 12 \\ Y _ { s c l } = 2 \end{array} D) \begin{array} { l } \theta _ { \min } = 0 \\ \theta _ { \max } = 2 \pi \\ \theta _ { s t e p } = \pi / 24 \\ X _ { \min } = - 12 \\ X _ { \max } = 12 \\ X _ { s c l } = 2 \\ Y _ { \min } = - 12 \\ Y _ { \max } = 12 \\ Y _ { s c l } = 2 \end{array} E) \begin{array} { l } \theta _ { \min } = 0 \\ \theta _ { \max } = 2 \pi \\ \theta _ { s t e p } = \pi / 24 \\ X _ { \min } = - 12 \\ X _ { \max } = 12 \\ X _ { s c l } = 2 \\ Y _ { \min } = - 12 \\ Y _ { \max } = 12 \\ Y _ { s c l } = 2 \end{array} θmin⁡=0θmax⁡=2πθstep=π/24Xmin⁡=−12Xmax⁡=12Xscl=2Ymin⁡=−12Ymax⁡=12Yscl=2\begin{array} { l } \theta _ { \min } = 0 \\\theta _ { \max } = 2 \pi \\\theta _ { s t e p } = \pi / 24 \\X _ { \min } = - 12 \\X _ { \max } = 12 \\X _ { s c l } = 2 \\Y _ { \min } = - 12 \\Y _ { \max } = 12 \\Y _ { s c l } = 2\end{array}
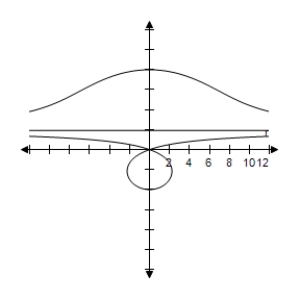
E) Select the correct graph of the polar equation.Describe your viewing window. r = 2 \csc \theta + 5 A) \begin{array} { l } \theta _ { \min } = 0 \\ \theta _ { \max } = 2 \pi \\ \theta _ { s t e p } = \pi / 24 \\ X _ { \min } = - 12 \\ X _ { \max } = 12 \\ X _ { s c l } = 2 \\ Y _ { \min } = - 12 \\ Y _ { \max } = 12 \\ Y _ { s c l } = 2 \end{array} B) \begin{array} { l } \theta _ { \min } = 0 \\ \theta _ { \max } = 2 \pi \\ \theta _ { s t e p } = \pi / 24 \\ X _ { \min } = - 12 \\ X _ { \max } = 12 \\ X _ { s c l } = 2 \\ Y _ { \min } = - 12 \\ Y _ { \max } = 12 \\ Y _ { s c l } = 2 \end{array} C) \begin{array} { l } \theta _ { \min } = 0 \\ \theta _ { \max } = 2 \pi \\ \theta _ { s t e p } = \pi / 24 \\ X _ { \min } = - 12 \\ X _ { \max } = 12 \\ X _ { s c l } = 2 \\ Y _ { \min } = - 12 \\ Y _ { \max } = 12 \\ Y _ { s c l } = 2 \end{array} D) \begin{array} { l } \theta _ { \min } = 0 \\ \theta _ { \max } = 2 \pi \\ \theta _ { s t e p } = \pi / 24 \\ X _ { \min } = - 12 \\ X _ { \max } = 12 \\ X _ { s c l } = 2 \\ Y _ { \min } = - 12 \\ Y _ { \max } = 12 \\ Y _ { s c l } = 2 \end{array} E) \begin{array} { l } \theta _ { \min } = 0 \\ \theta _ { \max } = 2 \pi \\ \theta _ { s t e p } = \pi / 24 \\ X _ { \min } = - 12 \\ X _ { \max } = 12 \\ X _ { s c l } = 2 \\ Y _ { \min } = - 12 \\ Y _ { \max } = 12 \\ Y _ { s c l } = 2 \end{array} θmin⁡=0θmax⁡=2πθstep=π/24Xmin⁡=−12Xmax⁡=12Xscl=2Ymin⁡=−12Ymax⁡=12Yscl=2\begin{array} { l } \theta _ { \min } = 0 \\\theta _ { \max } = 2 \pi \\\theta _ { s t e p } = \pi / 24 \\X _ { \min } = - 12 \\X _ { \max } = 12 \\X _ { s c l } = 2 \\Y _ { \min } = - 12 \\Y _ { \max } = 12 \\Y _ { s c l } = 2\end{array}

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q541: Consider a line with slope m and

Q542: Eliminate the parameter and write the

Q543: Eliminate the parameter and write the

Q544: A point (a,b) shown in below

Q545: Find the center and vertices of

Q547: Select the graph of the polar

Q548: Find the rectangular coordinates of the

Q549: Sketch the graph of the ellipse,

Q550: Find the vertex and focus of

Q551: Identify the conic by writing the