Both the Magnitude and Direction of the Force on a Crankshaft

Multiple Choice

Both the magnitude and direction of the force on a crankshaft change as the crankshaft rotates.Vectors representing the position of the crank and the force are $\mathbf { V } = 0.16 \left( - \cos 30 ^ { \circ } \mathbf { j } - \sin 30 ^ { \circ } \mathbf { k } \right)$ and $\mathbf { F } = - 2000 \mathrm { k }$ respectively.The magnitude of the torque on the crank is given by $\| \mathbf { V } \times \mathbf { F } \|$ ,find the magnitude of the torque on the crank shaft using the position and data shown in the figure. 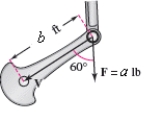$$\mathbf { a } = 2000 , \mathbf { b } = 0.16$$

A) $320 \sqrt { 3 } \mathrm { lt } - \mathrm { fb }$
B) $160 \mathrm { lt } - \mathrm { fb }$
C) $3201 \mathrm { t } - \mathrm { fb }$
D) $160 \sqrt { 3 } \mathrm { lt } - \mathrm { fb }$
E) $2000 \sqrt { 3 } \mathrm { lt } - \mathrm { fb }$