Multiple Choice
Find the limit (if it exists) .Use a graphing utility to verify your result graphically.
A) 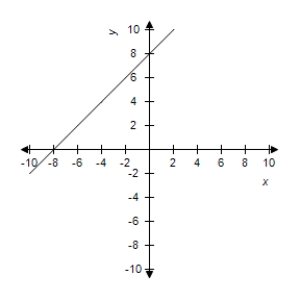
B) 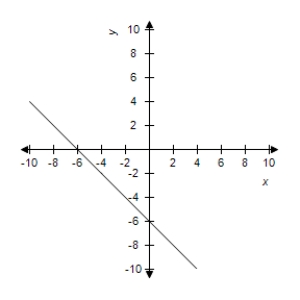
C) 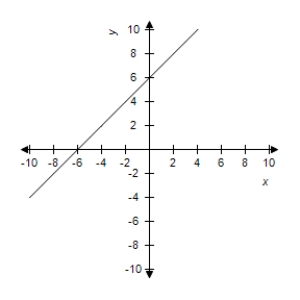
D) 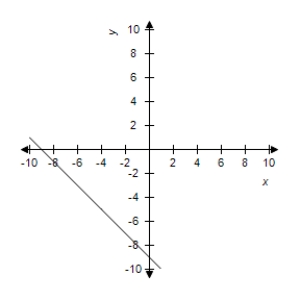
E) 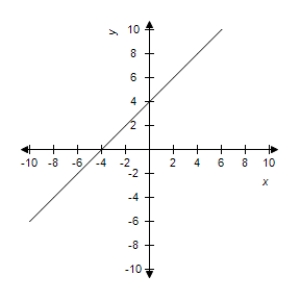
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q111: Determine what statement is true. <br>The exact
Q112: Use the first six terms to
Q113: Approximate the limit accurate to three
Q114: Find the limit. <br> <span
Q115: Find a formula for the slope
Q117: Find the derivative of the function.
Q118: Find the derivative of the function.
Q119: The cost function for a certain
Q120: Use the limit process to find
Q121: Use the derivative of <span