Multiple Choice
Find the limit (if it exists) .Use a graphing utility to verify your result graphically.
A) 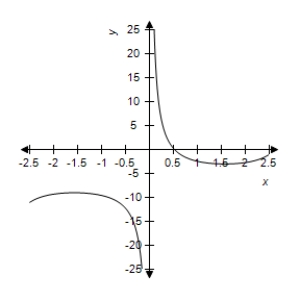
B) 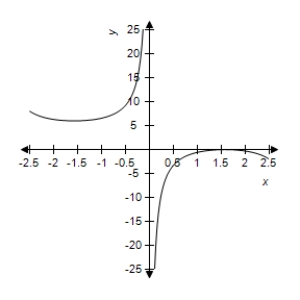
C) 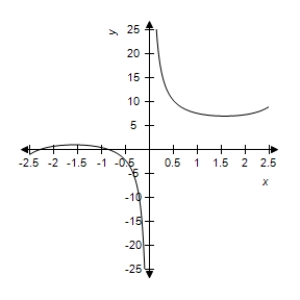
D) 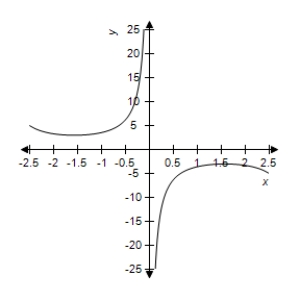
E) does not exist 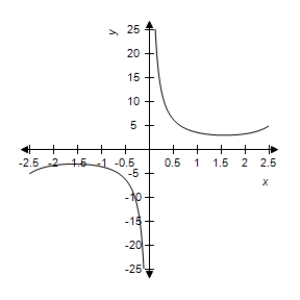
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q169: Use the limit process to find
Q170: Use asymptotes to match <span
Q171: Use the limit process to find
Q172: Given that <span class="ql-formula" data-value="\lim
Q173: Evaluate the sum using the summation
Q175: Algebraically evaluate the limit (if it
Q176: Select the correct function for the
Q177: The cost function for a company
Q178: Find the limit (if it exists).
Q179: Determine <span class="ql-formula" data-value="\lim _