Multiple Choice
Select the correct graph for the following function and find the limit (if it exists) as x approaches 2.
A) 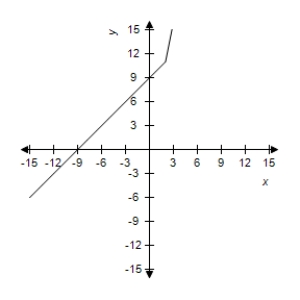 The limit exists as x approaches 2:
The limit exists as x approaches 2:
B) 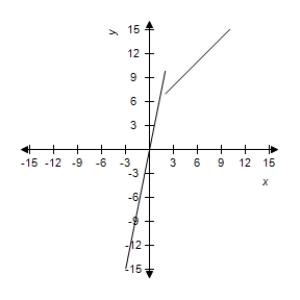 .
.
C) 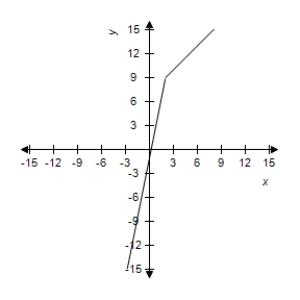
D) 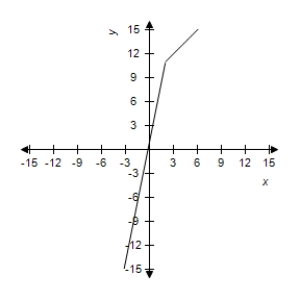 The limit exists as x approaches 2:
The limit exists as x approaches 2:
E) 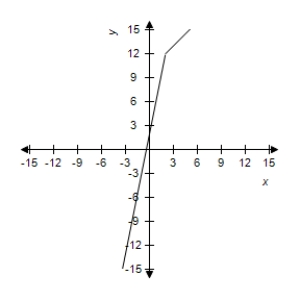 The limit exists as x approaches 2:
The limit exists as x approaches 2:
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q61: Find the limit by direct substitution.
Q62: Find a formula for the slope
Q63: Find <span class="ql-formula" data-value="\lim _
Q64: Evaluate <span class="ql-formula" data-value="\sum _
Q65: Find the limit (if it exists).
Q67: Find the limit (if it exists).Use
Q68: Select the correct graph for the
Q69: Use the graph to determine
Q70: Find the derivative of the function.
Q71: Find the derivative of <span