Multiple Choice
Select the correct graph for the following function and find the limit (if it exists) as x approaches 2.
A) 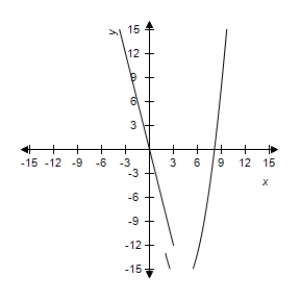 The limit exists as x approaches 2:
The limit exists as x approaches 2:
B)  The limit exists as x approaches 2:
The limit exists as x approaches 2:
C) 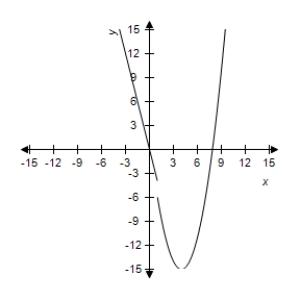 The limit exists as x approaches 2:
The limit exists as x approaches 2:
D) 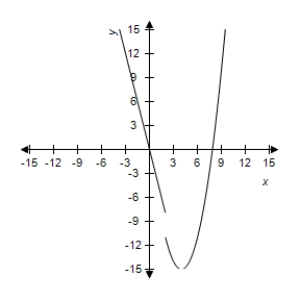
E) 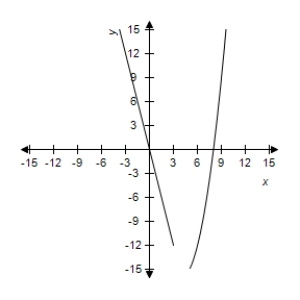 The limit exists as x approaches 2:
The limit exists as x approaches 2:
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q11: Use the first six terms to
Q12: Find <span class="ql-formula" data-value="\lim _
Q13: Evaluate the sum using the summation
Q14: Evaluate the sum using the summation
Q15: Use the limit process to find
Q17: Select the correct graph for the
Q18: Find a formula for the slope
Q19: Use the given information to evaluate
Q20: Use the position function <span
Q21: Find <span class="ql-formula" data-value="\lim _