Do Undergraduate Business Students Who Major in Information Systems (IS)

Essay

Do undergraduate business students who major in information systems (IS) earn, on average, higher annual starting salaries than their peers who major in marketing (Mktg)? To address this question with a statistical hypothesis test, a comparison should be done to determine whether the variances of annual starting salaries of the two types of majors are equal. Below you will find output from a test of 20 randomly selected IS majors and 20 randomly selected Mktg majors.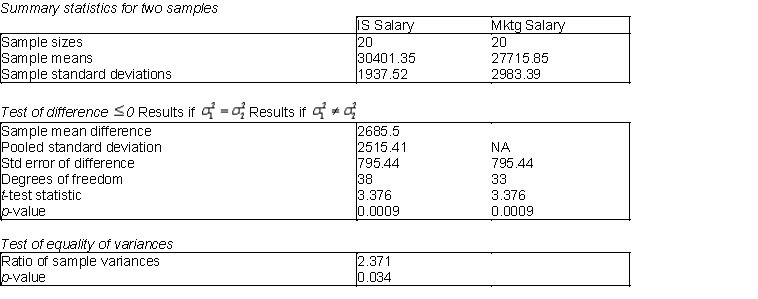
-(A) Use the information above to perform the test of equal variance. Explain how the ratio of sample variances is calculated. What type of distribution is used to test for equal variances? Also, would you conclude that the variances are equal or not? Explain.
​
(B) Based on your conclusion in (A), which test statistic should be used in performing a test for the existence of a difference between population means?
​
(C) Using a 5% level of significance, is there sufficient evidence to conclude that IS majors earn, on average, a higher annual starting salaries than their peers who major in Mktg?
​
(D) Using a 1% level of significance, is there sufficient evidence to conclude that IS majors earn, on average, a higher annual starting salaries than their peers who major in Mktg? Explain your answer.