Suppose That a Recent Study Shows That Each Week Each

Essay

Suppose that a recent study shows that each week each of 300 families buys a gallon of apple juice from company A, B, or C. Let 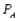denote the probability that a gallon produced by company A is of unsatisfactory quality, and define 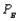and similarly for companies B and C. If the last gallon of juice purchased by a family is satisfactory, the next week they will purchase a gallon of juice from the same company. If the last gallon of juice purchased by a family is not satisfactory, then the family will purchase a gallon from a competitor. Consider one week in which A families have purchased juice A, B families have purchased juice B, and C families have purchased juice C. Assume that families that switch brands during a period are allocated to the remaining brands in a manner that is proportional to the current market shares of the other brands. Thus, if a customer switches from brand A, there is probability B/(B + C) that he will switch to brand B and probability C/(B + C) that he will switch to brand C. Suppose that the market is currently divided equally: 100 families for each of the three brands.
-After a year, what will the market share for each of the three companies be? Assume 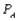= 0.10, 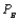= 0.15, and 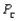= 0.20. (Hint: Use the RISKBINOMIAL function to model how many people switch from A, then how many switch from A to B and from A to C.)