Multiple Choice
Solve the inequality and graph. Express your answer in interval notation.
--4(-2 - x) < 6x + 19 - 11 - 2x 
A) 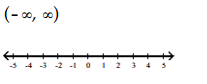
B) 
C) 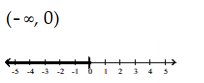
D) 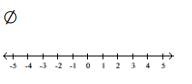
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q26: Provide an appropriate response.<br>-Find the standard form
Q28: Solve the problem.<br>-At a local grocery store
Q30: Solve the problem.<br>-Suppose the sales of a
Q32: Solve the problem.<br>-Using a phone card to
Q35: Find the slope and y intercept of
Q36: Use the graph to find the average
Q37: Solve the problem.<br>-The cost of manufacturing a
Q42: Provide an appropriate response.<br>-Find the line passing
Q55: Provide an appropriate response.<br>-Write the equation of
Q67: Provide an appropriate response.<br>-Find the standard form